题目内容
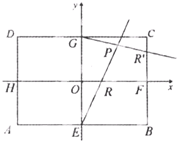 (2013•黄冈模拟)在矩形ABCD中,|AB|=2
(2013•黄冈模拟)在矩形ABCD中,|AB|=2| 3 |
| |OR| |
| |OF| |
| |CR′| |
| |OF| |
| 1 |
| n |
(Ⅰ)求证:直线ER与GR′的交点P在椭圆Ω:
| x2 |
| 3 |
(Ⅱ)若M、N为椭圆Ω上的两点,且直线GM与直线GN的斜率之积为
| 2 |
| 3 |
分析:(Ⅰ)由且
=
=
求出R和R′的坐标,求出直线GR′和直线ER的方程,联立求出交点,把交点坐标代入椭圆方程进行验证;
(Ⅱ)设出M,N的坐标,当直线斜率存在时,设出直线方程,和椭圆方程联立,利用根与系数关系求出M,N两点坐标的和与积,代入斜率公式,求得MN的斜率和截距的关系,由纤细方程证明结论,当斜率不存在时,直接求出M,N的坐标验证.
| |OR| |
| |OF| |
| |CR′| |
| |OF| |
| 1 |
| n |
(Ⅱ)设出M,N的坐标,当直线斜率存在时,设出直线方程,和椭圆方程联立,利用根与系数关系求出M,N两点坐标的和与积,代入斜率公式,求得MN的斜率和截距的关系,由纤细方程证明结论,当斜率不存在时,直接求出M,N的坐标验证.
解答:证明:(Ⅰ)如图,
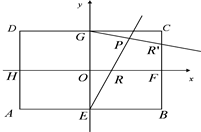
∵
=
=
,∴R(
,0),R′(
,
),
又G(0,1),则直线GR′的方程为y=-
x+1 ①
又E(0,-1),则直线ER的方程为y=
x-1 ②
由①②得P(
,
),代入椭圆方程得:
+(
)2=
=1.
∴直线ER与GR′的交点P在椭圆Ω:
+y2=1上;
(Ⅱ)①当直线MN的斜率不存在时,设MN:x=t(-
<t<
),
则M(t,
),N(t,-
),∴kGM•kGN=
,不合题意.
②当直线MN的斜率存在时,设MN:y=kx+b,
M(x1,y1),N(x2,y2),

联立方程
,
得(1+3k2)x2+6kbx+3b2-3=0.
则△=12(3k2-b2+1)>0,
x1+x2=
,x1x2=
,
又kGM•kGN=
•
=
=
,
即(3k2-2)x1x2+3k(b-1)(x1+x2)+3(b-1)2=0,
将x1+x2=
,x1x2=
代入上式得b=-3,
∴直线过定点T(0,-3).

∵
| |OR| |
| |OF| |
| |CR′| |
| |CF| |
| 1 |
| n |
| ||
| n |
| 3 |
| n-1 |
| n |
又G(0,1),则直线GR′的方程为y=-
| 1 | ||
|
又E(0,-1),则直线ER的方程为y=
| n | ||
|
由①②得P(
2
| ||
| n2+1 |
| n2-1 |
| n2+1 |
(
| ||||
| 3 |
| n2-1 |
| n2+1 |
| 4n2+(n2-1)2 |
| (n2+1)2 |
∴直线ER与GR′的交点P在椭圆Ω:
| x2 |
| 3 |
(Ⅱ)①当直线MN的斜率不存在时,设MN:x=t(-
| 3 |
| 3 |
则M(t,
1-
|
1-
|
| 1 |
| 3 |
②当直线MN的斜率存在时,设MN:y=kx+b,
M(x1,y1),N(x2,y2),

联立方程
|
得(1+3k2)x2+6kbx+3b2-3=0.
则△=12(3k2-b2+1)>0,
x1+x2=
| -6kb |
| 1+3k2 |
| 3b2-3 |
| 1+3k2 |
又kGM•kGN=
| y1-1 |
| x1 |
| y2-1 |
| x2 |
| k2x1x2+k(b-1)(x1+x2)+(b-1)2 |
| x1x2 |
| 2 |
| 3 |
即(3k2-2)x1x2+3k(b-1)(x1+x2)+3(b-1)2=0,
将x1+x2=
| -6kb |
| 1+3k2 |
| 3b2-3 |
| 1+3k2 |
∴直线过定点T(0,-3).
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,训练了两直线交点坐标的求法,考查了由两点求直线的斜率公式,考查了学生的计算能力,是有一定难度题目.

练习册系列答案
相关题目
 (2013•黄冈模拟)如图所示程序框图的输出的所有值都在函数( )
(2013•黄冈模拟)如图所示程序框图的输出的所有值都在函数( )