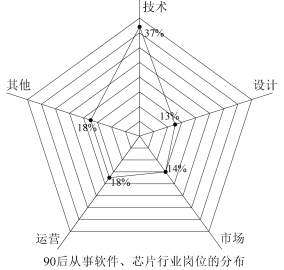
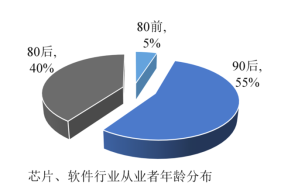
题目内容
【题目】如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
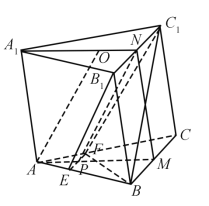
(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱锥B–EB1C1F的体积.
,求四棱锥B–EB1C1F的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,根据条件可得
,根据条件可得![]() ,可证
,可证![]() ,要证平面
,要证平面![]()
![]() 平面
平面![]() ,只需证明
,只需证明![]() 平面
平面![]() 即可;
即可;
(2)根据已知条件求得![]() 和
和![]() 到
到![]() 的距离,根据椎体体积公式,即可求得
的距离,根据椎体体积公式,即可求得![]() .
.
(1)![]()
![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
![]()
又![]()
![]()
在等边![]() 中,
中,![]() 为
为![]() 中点,则
中点,则![]()
又![]() 侧面
侧面![]() 为矩形,
为矩形,
![]()
![]()
![]()
由![]() ,
,![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
又![]()
![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
又![]()
![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
![]()
![]()
又![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
(2)过![]() 作
作![]() 垂线,交点为
垂线,交点为![]() ,
,
画出图形,如图
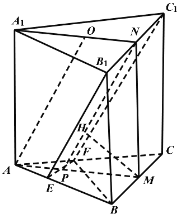
![]()
![]() 平面
平面![]()
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]() 为
为![]() 的中心.
的中心.
![]()
![]()
故:![]() ,则
,则![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
又![]() 在等边
在等边![]() 中
中![]()
即![]()
由(1)知,四边形![]() 为梯形
为梯形
![]() 四边形
四边形![]() 的面积为:
的面积为:![]()
![]() ,
,
![]() 为
为![]() 到
到![]() 的距离
的距离![]() ,
,
![]()
![]() .
.

 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
【题目】某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 40 | 20 | 20 | 20 |
乙分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 28 | 17 | 34 | 21 |
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?