题目内容
10．已知F是抛物线C：y2=2px（p＞0）的焦点，过点R（2，1）的直线l与抛物线C交于A、B两点，且|RA|=|RB|，|FA|+|FB|=5，则直线l的斜率为（ ）| A． | $\frac{3}{2}$ | B． | 1 | C． | 2 | D． | $\frac{1}{2}$ |
分析 设出A，B的坐标，代入抛物线方程，由点差法得到直线AB的斜率，结合R为AB的中点及抛物线的焦半径公式得答案．
解答 解：设A（x1，y1），B（x2，y2），
则点R（2，1）为线段AB的中点，x1+x2=4，y1+y2=2，
y12=2px1，y22=2px2，
作差整理得：$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2p}{{y}_{1}+{y}_{2}}$=p，
即直线AB的斜率k=$\frac{2p}{2}$=p．
又|FA|+|FB=5，
∴x1+x2+p=5，即4+p=5，p=1．
∴k=1．
故选：B．
点评 本题考查了抛物线的几何性质，考查了转化思想，是中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
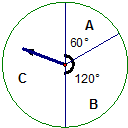五一节期间，某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券．（假定指针等可能地停在任一位置，指针落在区域的边界时，重新转一次）指针所在的区域及对应的返劵金额见右上表．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
2．已知集合A={x|$\frac{1}{x-2}＜1$}，B={x||x-1|≤2}，则A∩B=（ ）
| A． | （-∞，1）∪[2，3） | B． | [-1，2） | C． | （-∞，-1）∪[2，3）∪（3，+∞） | D． | （-∞，-1）∪（3，+∞） |