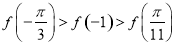题目内容
1.求下列关于x的不等式的解集.(1)(1+x)(1-|x|)>0;
(2)$\sqrt{4x{-x}^{2}}$<x;
(3)$\frac{x-1}{x}$≥2;
(4)f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+6,x≥0}\\{x+6,x<0}\end{array}\right.$,f(x)>f(1);
(5)f(x)=$\left\{\begin{array}{l}{{2}^{-x}-1,x≤0}\\{{x}^{\frac{1}{2}},x>0}\end{array}\right.$,f(x)>f(1)
分析 分别根据不等式的解法进行求解即可.
解答 解:(1)若x≥0,则不等式等价为(1+x)(1-x)>0,即(1+x)(x-1)<0,解得-1<x<1,此时0≤x<1,
若x<0,则不等式等价为(1+x)(1+x)>0,即x≠-1,此时x<0且x≠-1;
综上不等式的解为x<1且x≠-1,即不等式的解集为{x|x<1且x≠-1}.
(2)由$\sqrt{4x{-x}^{2}}$<x得$\left\{\begin{array}{l}{x≥0}\\{4x-{x}^{2}≥0}\\{4x-{x}^{2}<{x}^{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{x≥0}\\{0≤x≤4}\\{x>2或x<0}\end{array}\right.$,解得2<x≤4,即不等式的解集为(2,4];
(3)由$\frac{x-1}{x}$≥2得$\frac{x-1}{x}$-2=$\frac{-1-x}{x}$≥0,即$\frac{x+1}{x}≤0$,解得-1≤x<0,即不等式的解集为[-1,0);
(4)∵f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+6,x≥0}\\{x+6,x<0}\end{array}\right.$,∴f(1)=1-4+6=3,
当x≥0是,由f(x)>3得x2-4x+6>3,即x2-4x+3>0,解得x>3或x<1,此时x>3或0≤x<1,
当x<0是,由f(x)>3得x+6>3,即x>-3,解得-3<x<0,
综上x>3或-3<x<1,即不等式的解集为{x|x>3或-3<x<1};
(5)∵f(x)=$\left\{\begin{array}{l}{{2}^{-x}-1,x≤0}\\{{x}^{\frac{1}{2}},x>0}\end{array}\right.$,∴f(1)=1,
当x>0时,由f(x)>1得$\sqrt{x}>1$,解得x>1,
当x≤0时,由f(x)>1得2-x-1>1.即2-x>2,解得-x>1,即x<-1,
综上x>1或x<-1,
即不等式的解集为{x|x>1或x<-1}.
点评 本题主要考查不等式的求解,要求熟练掌各种不等式的解法.

| A. | (-1,3) | B. | (-3,1) | C. | (3,+∞) | D. | (-∞,1) |
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
 ,则
,则 的大小关系为( )
的大小关系为( )