题目内容
定义在R上的连续函数g(x)满足:当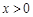 时,
时, 恒成立(
恒成立( 为函数
为函数 的导函数);对任意的
的导函数);对任意的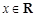 都有
都有 .函数
.函数 满足:对任意的
满足:对任意的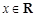 ,都有
,都有 成立;当
成立;当 时
时 .若关于
.若关于 的不等式
的不等式 对
对 恒成立. 则
恒成立. 则 的取值范围是
的取值范围是
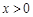 时,
时, 恒成立(
恒成立( 为函数
为函数 的导函数);对任意的
的导函数);对任意的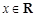 都有
都有 .函数
.函数 满足:对任意的
满足:对任意的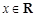 ,都有
,都有 成立;当
成立;当 时
时 .若关于
.若关于 的不等式
的不等式 对
对 恒成立. 则
恒成立. 则 的取值范围是
的取值范围是A. R R |
B. |
C. 或 或 |
D. |
C
试题分析:
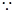 当
当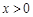 时,
时, 恒成立(
恒成立( 为函数
为函数 的导函数),
的导函数),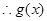 在
在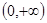 单调递增;
单调递增;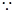 对任意的都有
对任意的都有 ,
,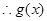 为偶函数;即
为偶函数;即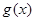 在
在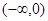 递减.
递减.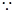 关于
关于 的不等式
的不等式 对
对 恒成立,即
恒成立,即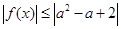 对
对 恒成立,即
恒成立,即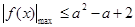 .
.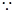 对任意的
对任意的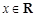 ,都有
,都有 成立,
成立,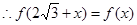 ,即
,即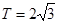 ;
;当
 时,
时, ,
,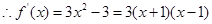 ,且
,且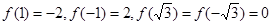 ,即在
,即在 ,
,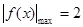 .
.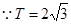 ,对
,对 ,
,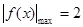 .
. 因此
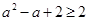 ,即
,即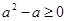 ,
,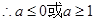 .
.
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
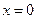 处连续的是
处连续的是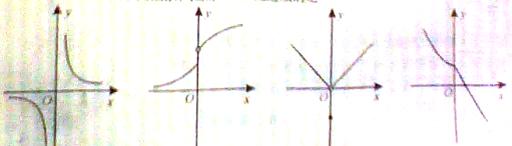

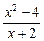 ,
,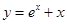 在点(0,1)处的切线方程为 .
在点(0,1)处的切线方程为 .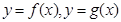 的导函数的图像如下图,那么
的导函数的图像如下图,那么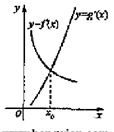

 在点
在点 处的切线的方程为___________
处的切线的方程为___________ 在
在 处的切线的斜率为 .
处的切线的斜率为 .