题目内容
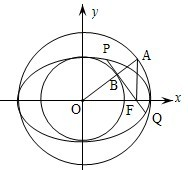 如图,以椭圆
如图,以椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求证c2=ab,并求直线BF与y轴的交点M的坐标;
(2)设直线BF交椭圆于P、Q两点,求证
| OP |
| OQ |
| 1 |
| 2 |
分析:(1)直接利用Rt△OFA∽Rt△OBF,找到对应边的比值相等即可证明c2=ab,再求出直线OA的斜率,利用OA与直线BF垂直可得直线BF的斜率,进而求出直线BF的方程以及BF与y轴的交点M的坐标;
(2)先把直线BF的方程与椭圆方程联立,求出关于P、Q两点的坐标以及直线BF的斜率之间的等量关系,代入
•
整理可得结论.(注意整理过程中要细心)
(2)先把直线BF的方程与椭圆方程联立,求出关于P、Q两点的坐标以及直线BF的斜率之间的等量关系,代入
| OP |
| OQ |
解答:解:(1)由题设条件知,Rt△OFA∽Rt△OBF,
故
=
,即
=
,因此c2=ab.①(2分)
在Rt△OFA中,FA=
=
=b
于是,直线OA的斜KOA=
.设直线BF的斜率为k,k=-
=-
.
所以直线BF的方程为:y=-
(x-c)(5分)
直线BF与y轴的交点为M(0,
)即(0,a).(6分)
(2)由(1),得直线BF得方程为y=kx+a,k2=
=
=
②
由已知,P(x1,y1),Q(x2,y2),则它们的坐标满足方程
③
由方程组③消y,并整理得(b2+a2k2)x2+2a3x2+2a3kx+a4-a2b2=0,④
由式①、②和④,x1x2=
+
=
=
.x1+x2=
综上,得到
•
=x1x2+y1y2=
,(12分)
又因a2-ab+b2=a2-c2+b2=2b2,得
(15分)
故
| OF |
| OA |
| OB |
| OF |
| c |
| a |
| b |
| c |
在Rt△OFA中,FA=
| OA2-OF2 |
| a2-c2 |
于是,直线OA的斜KOA=
| b |
| c |
| 1 |
| kOA |
| c |
| b |
所以直线BF的方程为:y=-
| c |
| b |
直线BF与y轴的交点为M(0,
| c2 |
| b |
(2)由(1),得直线BF得方程为y=kx+a,k2=
| c2 |
| a2 |
| ab |
| a2 |
| a |
| b |
由已知,P(x1,y1),Q(x2,y2),则它们的坐标满足方程
|
由方程组③消y,并整理得(b2+a2k2)x2+2a3x2+2a3kx+a4-a2b2=0,④
由式①、②和④,x1x2=
| a4-a2b2 |
| b2+a2k2 |
| a2(a2-b2) | ||
b2+a2
|
| a2c2 | ||
b2+
|
| a3b2 |
| b3+a3 |
| -2a3k |
| b2+a2k2 |
|
综上,得到
| OP |
| OQ |
| a2b3 |
| a3+b3 |
又因a2-ab+b2=a2-c2+b2=2b2,得
|
点评:本题是对椭圆与圆以及直线与椭圆位置关系的综合考查.这一类型题目,思路比较清晰,就是整理过程要求比较高,所以在做题时,一定要认真,细致.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
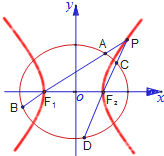 如图,已知椭圆
如图,已知椭圆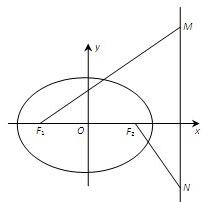 如图,椭圆
如图,椭圆
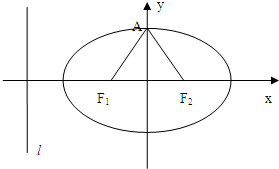 如图,椭圆C:
如图,椭圆C: