题目内容

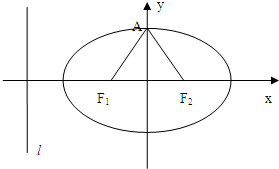如图，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点F1、F2和短轴的一个端点A构成等边三角形，点（
3
，
3
2
）在椭圆C上，直线l为椭圆C的左准线，
（1）求椭圆C的方程；
（2）设P是椭圆C上的点，作PQ⊥l，垂足为Q，以Q为圆心，PQ为半径作圆Q，当点F1在该圆上时，求圆的方程．
分析：（1）根据正三角形的性质可知b=
3
c，进而根据a，b和c的关系进而求得a和c的关系，将点（
3
，
3
2
）的坐标代入椭圆方程中，得c，则椭圆的方程可得．
（2）欲求圆的方程，关键是求出其圆心坐标和半径．设P点坐标（x，y），则Q点坐标（-4，y）由PQ=F1Q，|x+4|=
(4-1)2+y2
，平方化简得x2+8x-y2+7=0与椭圆方程解得P，从而求出半径及圆心．
解答：解：（1）依题意可知b=
3
c
∴a=
b2+c2
=2c
∴椭圆方程变为：
x2
4c2
+
y2
3c2
=1，
将点（
3
，
3
2
）的坐标代入椭圆方程中，得
(
3
)2
4c2
+
(
3
2
)2
3c2
=1，
∴c=1，
故椭圆方程
x2
4
+
y2
3
=1，
（2）设P点坐标（x，y），则Q点坐标（-4，y）
由PQ=F1Q，|x+4|=
(4-1)2+y2
，
平方化简得x2+8x-y2+7=0与椭圆方程解得P（-
4
7
，±
3
15
7
），即Q的坐标为（-4，±
3
15
7
）
r=4-
4
7
=
24
7
，
所求圆方程为(x+4)2+(y±
3
15
7
)2=
576
49
．
点评：本题主要考查了圆的标准方程、椭圆的简单性质，考查了学生对椭圆基础知识的把握和理解，考查了方程思想．
练习册系列答案
相关题目
精英家教网如图，椭圆C：
x2
a2
+
y2
2
=1焦点在x轴上，左、右顶点分别为A1、A，上顶点为B，抛物线C1、C2分别以A、B为焦点，其顶点均为坐标原点O．C1与C2相交于直线y=
2
x上一点P．
（Ⅰ）求椭圆C及抛物线C1、C2的方程；
（Ⅱ）若动直线l与直线OP垂直，且与椭圆C交于不同两点M、N，已知点Q(-
2
，0），求
QM
.
QN
的最小值．
（2008•闸北区二模）如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，A1、A2为椭圆C的左、右顶点．
（Ⅰ）设F1为椭圆C的左焦点，证明：当且仅当椭圆C上的点P在椭圆的左、右顶点时|PF1|取得最小值与最大值；
（Ⅱ）若椭圆C上的点到焦点距离的最大值为3，最小值为1．求椭圆C的标准方程；
（Ⅲ）若直线l：y=kx+m与（Ⅱ）中所述椭圆C相交于A，B两点（A，B不是左右顶点），且满足AA2⊥BA2，求证：直线l过定点，并求出该定点的坐标．
如图，椭圆C：
x2
a2
+
y2
a2-1
=1的左右顶点分别为A、B，左右焦点分别为F1、F2，P为以F1、F2为直径的圆上异于F1、F2的动点，直线PF1、PF2分别交椭圆C于M、N和D、E．
（1）证明：
AP
•
BP
为定值K；
（2）当K=-2时，问是否存在点P，使得四边形DMEN的面积最小，若存在，求出最小值和P坐标，若不存在，请说明理由．
如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的顶点为A1、A2、B1、B2，焦点为F1，
F2，|A1B1|=
7
，
S?A1B1A2B 2=2S?B1F1B2F 2
（1）求椭圆C的方程；
（2）设l是过原点的直线，直线n与l垂直相交于P点，且n与椭圆相交于A，B两点，|OP|=1，求
AP
•
PB
的取值范围．
（2011•重庆三模）光线被曲线反射，等效于被曲线在反射点处的切线反射．已知光线从椭圆的一个焦点出发，被椭圆反射后要回到椭圆的另一个焦点；光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出；如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)与双曲线C′：
x2
m2
-
y2
n2
=1(m＞0，n＞0)有公共焦点，现一光线从它们的左焦点出发，在椭圆与双曲线间连续反射，则光线经过2k（k∈N*）次反射后回到左焦点所经过的路径长为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网