题目内容
如图,某隧道设计为双向四车道,车道总宽20m,要求通行车辆限高5m,隧道全长2.5km,隧道的两侧是与地面垂直的墙,高度为3米,隧道上部拱线近似地看成半个椭圆.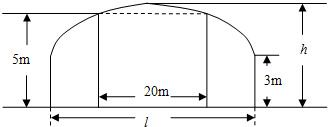
(1)若最大拱高h为6m,则隧道设计的拱宽l是多少?
(2)若要使隧道上方半椭圆部分的土方工程量最小,则应如何设计拱高h和拱宽l?
(已知:椭圆
| x2 |
| a2 |
| y2 |
| b2 |
(3)为了使隧道内部美观,要求在拱线上找两个点M、N,使它们所在位置的高度恰好是限高5m,现以M、N以及椭圆的左、右顶点为支点,用合金钢板把隧道拱线部分连接封闭,形成一个梯形,若l=30m,梯形两腰所在侧面单位面积的钢板造价是梯形顶部单位面积钢板造价的
| 2 |
分析:(1)先建立直角坐标系,找到对应椭圆方程再把b=h-3=3与点P坐标代入椭圆方程,即可求出隧道设计的拱宽l是多少;
(2)转化为求半椭圆的面积最小值问题,对椭圆方程用基本不等式即可求出对应的半椭圆面积以及满足要求的拱高h和拱宽l.
(3)先求出总造价的表达式,再利用导函数研究其最值即可.
(2)转化为求半椭圆的面积最小值问题,对椭圆方程用基本不等式即可求出对应的半椭圆面积以及满足要求的拱高h和拱宽l.
(3)先求出总造价的表达式,再利用导函数研究其最值即可.
解答: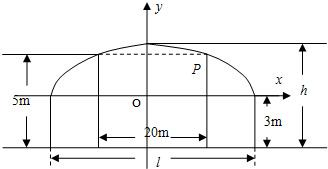 解:(1)如图建立直角坐标系,
解:(1)如图建立直角坐标系,
则点P(10,2),椭圆方程为
+
=1.
将b=h-3=3与点P坐标代入椭圆方程,
得a=6
,此时l=2a=12
,
因此隧道的拱宽约为12
m.(5分)
(2)要使隧道上方半椭圆部分的土方工程量最小,
由柱体的体积公式可知:只需半椭
圆的面积最小即可.
由椭圆方程
+
=1,得
+
=1.
因为
+
≥
,即ab≥40,(8分)
所以半椭圆面积S=
≥
=20π.(10分)
当S取最小值时,有
=
=
,得a=10
,b=2
.
此时l=2a=20
,h=b+3=2
+3(12分)
故当拱高为(2
+3)m、拱宽为20
m时,
隧道上方半椭圆部分的土方工程量最小(13分)
(3)根据题意设M(x,2),N(-x,2),则10≤x<15
设f(x)=2x+2
=2[x+
],(10≤x<15)(11分)
则f′(x)=
令f'(x)=0,?x2-30x+221=0?x=13(x=17舍去),
且10≤x<13时,f′(x)<0,13<x<15时,f′(x)>0,
∴x=13时,f(x)取最小值,此时M(13,2),N(-13,2),
代入椭圆方程得b=
∴h=3+b=3+
(13分)
 解:(1)如图建立直角坐标系,
解:(1)如图建立直角坐标系,则点P(10,2),椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
将b=h-3=3与点P坐标代入椭圆方程,
得a=6
| 5 |
| 5 |
因此隧道的拱宽约为12
| 5 |
(2)要使隧道上方半椭圆部分的土方工程量最小,
由柱体的体积公式可知:只需半椭
圆的面积最小即可.
由椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
| 102 |
| a2 |
| 22 |
| b2 |
因为
| 102 |
| a2 |
| 22 |
| b2 |
| 2×10×2 |
| ab |
所以半椭圆面积S=
| πab |
| 2 |
| 40π |
| 2 |
当S取最小值时,有
| 102 |
| a2 |
| 22 |
| b2 |
| 1 |
| 2 |
| 2 |
| 2 |
此时l=2a=20
| 2 |
| 2 |
故当拱高为(2
| 2 |
| 2 |
隧道上方半椭圆部分的土方工程量最小(13分)
(3)根据题意设M(x,2),N(-x,2),则10≤x<15
设f(x)=2x+2
| 2 |
| (x-15)2+(2-0)2 |
=2[x+
| 2(x2-30x+299) |
则f′(x)=
2[
| ||||
|
令f'(x)=0,?x2-30x+221=0?x=13(x=17舍去),
且10≤x<13时,f′(x)<0,13<x<15时,f′(x)>0,
∴x=13时,f(x)取最小值,此时M(13,2),N(-13,2),
代入椭圆方程得b=
25
| ||
| 14 |
∴h=3+b=3+
25
| ||
| 14 |
点评:本题是对椭圆方程在实际生活中应用的考查.涉及到了函数的最值问题.一般在研究函数的最值问题时,通常借助于导函数.

练习册系列答案
相关题目
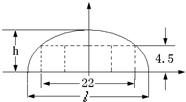 如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.
如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.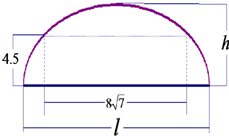 如图,某隧道设计为双向四车道,车道总宽为
如图,某隧道设计为双向四车道,车道总宽为
