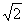题目内容
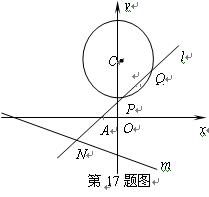
已知过点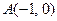 的动直线
的动直线 与圆
与圆 :
: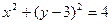 相交于
相交于 、
、 两点,
两点,  与
与
直线 :
: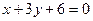 相交于
相交于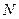 .
.
(1)求证:当 与
与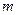 垂直时,
垂直时, 必过圆心
必过圆心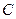 ;
;
(2)当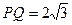 时,求直线
时,求直线 的方程.
的方程.
 的动直线
的动直线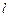 与圆
与圆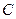 :
: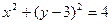 相交于
相交于 、
、 两点,
两点,  与
与直线
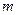 :
: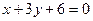 相交于
相交于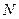 .
.(1)求证:当
 与
与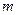 垂直时,
垂直时, 必过圆心
必过圆心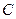 ;
;(2)当
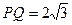 时,求直线
时,求直线 的方程.
的方程.
(2)直线 的方程为
的方程为 或
或
 的方程为
的方程为 或
或
(1)∵ 与
与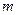 垂直,且
垂直,且 ,∴
,∴ ,
,
故直线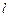 方程为
方程为 ,即
,即 ………3分
………3分
∵圆心坐标(0,3)满足直线 方程,
方程,
∴当 与
与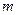 垂直时,
垂直时, 必过圆心
必过圆心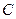 …………………5分
…………………5分
(2)①当直线 与
与 轴垂直时, 易知
轴垂直时, 易知 符合题意………8分
符合题意………8分
②当直线 与
与 轴不垂直时, 设直线
轴不垂直时, 设直线 的方程为
的方程为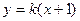 ,即
,即 ,……9分
,……9分
∵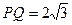 ,∴
,∴ ,……………10分
,……………10分
则由 ,得
,得 , ∴直线
, ∴直线 :
: .………13分
.………13分
故直线 的方程为
的方程为 或
或 …………………14分
…………………14分

 与
与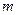 垂直,且
垂直,且 ,∴
,∴ ,
,故直线
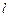 方程为
方程为 ,即
,即 ………3分
………3分∵圆心坐标(0,3)满足直线
 方程,
方程,∴当
 与
与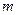 垂直时,
垂直时, 必过圆心
必过圆心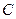 …………………5分
…………………5分(2)①当直线
 与
与 轴垂直时, 易知
轴垂直时, 易知 符合题意………8分
符合题意………8分②当直线
 与
与 轴不垂直时, 设直线
轴不垂直时, 设直线 的方程为
的方程为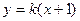 ,即
,即 ,……9分
,……9分∵
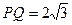 ,∴
,∴ ,……………10分
,……………10分则由
 ,得
,得 , ∴直线
, ∴直线 :
: .………13分
.………13分故直线
 的方程为
的方程为 或
或 …………………14分
…………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与圆
与圆 交于
交于 两点,且
两点,且 对称,求不等式组
对称,求不等式组 表示的平面区域的面积
表示的平面区域的面积


 ,椭圆C2的方程为
,椭圆C2的方程为 =1(a>b>0),C2的离心率为
=1(a>b>0),C2的离心率为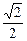 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
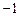 ),B(5,3),并且被直线
),B(5,3),并且被直线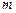 :
: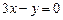 平分圆的面积.
平分圆的面积.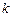 的直线
的直线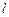 与圆C有两个不同的公共点,求实数
与圆C有两个不同的公共点,求实数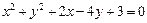
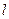 与圆C相切,且直线
与圆C相切,且直线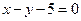 距离的最大值与最小值
距离的最大值与最小值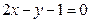 被圆
被圆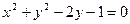 所截得的弦长为 .
所截得的弦长为 .