题目内容
数列{an}的首项a1=1,前n项和为Sn,且3tSn-(2t+3)Sn-1=3t(t为常数, ,t≠0,n≥2)
,t≠0,n≥2)(1)求证:{an}是等比数列;
(2)设{an}的公比为f(t),数列{bn}(满足b1=1,
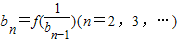 ,求bn;
,求bn;(3)数列{cn}的通项为
 ,那么是否存在实数t,使得数列{(-1)ncn+cn+1}中的每一项都大于1?若存在,求出t的范围;若不存在,请说明理由.
,那么是否存在实数t,使得数列{(-1)ncn+cn+1}中的每一项都大于1?若存在,求出t的范围;若不存在,请说明理由.
【答案】分析:(1)由题意得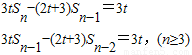 ,由此能够证明:{an}是等比数列.
,由此能够证明:{an}是等比数列.
(2)由 ,知
,知 .
.
(3)由 ,当n为奇数时,
,当n为奇数时,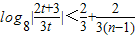 对所有奇数成立;当n为偶数时,
对所有奇数成立;当n为偶数时, 对所有偶数成立,由此能够求出存在满足条件的实数t,t>6或
对所有偶数成立,由此能够求出存在满足条件的实数t,t>6或 且
且 .
.
解答:解:(1)由题意,可得
 ,
,
两式相减,得3tan-(2t+3)an-1=0,
即
又3t(1+a2)-(2t+3)=3t,
∴ ,
,
∴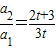
所以,{an}是以1为首项, 为公比的等比数列;
为公比的等比数列;
(2)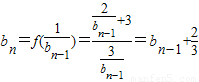 ,
,
∴ ;
;
(3)
①当n为奇数时,
若存在满足条件的t,
则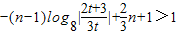 对所有奇数成立,
对所有奇数成立,
即 对所有奇数成立,
对所有奇数成立,
所以 ,
,
∴ 或
或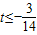
②当n为偶数时,
若存在满足条件的t,则 对所有偶数成立,
对所有偶数成立,
即 对所有偶数成立,
对所有偶数成立,
所以 ,
,
∴t>6或
综合之,存在满足条件的实数t,t>6或 且
且 .
.
点评:本题考查不等式和数列的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
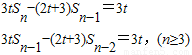 ,由此能够证明:{an}是等比数列.
,由此能够证明:{an}是等比数列.(2)由
 ,知
,知 .
.(3)由
 ,当n为奇数时,
,当n为奇数时,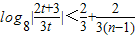 对所有奇数成立;当n为偶数时,
对所有奇数成立;当n为偶数时, 对所有偶数成立,由此能够求出存在满足条件的实数t,t>6或
对所有偶数成立,由此能够求出存在满足条件的实数t,t>6或 且
且 .
.解答:解:(1)由题意,可得
 ,
,两式相减,得3tan-(2t+3)an-1=0,
即

又3t(1+a2)-(2t+3)=3t,
∴
 ,
,∴
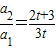
所以,{an}是以1为首项,
 为公比的等比数列;
为公比的等比数列;(2)
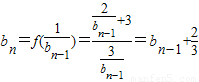 ,
,∴
 ;
;(3)

①当n为奇数时,

若存在满足条件的t,
则
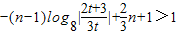 对所有奇数成立,
对所有奇数成立,即
 对所有奇数成立,
对所有奇数成立,所以
 ,
,∴
 或
或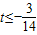
②当n为偶数时,

若存在满足条件的t,则
 对所有偶数成立,
对所有偶数成立,即
 对所有偶数成立,
对所有偶数成立,所以
 ,
,∴t>6或

综合之,存在满足条件的实数t,t>6或
 且
且 .
.点评:本题考查不等式和数列的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目