题目内容
(2013•青岛二模)已知数列{an}是以3为公差的等差数列,Sn是其前n项和,若S10是数列{Sn}中的唯一最小项,则数列{an}的首项a1的取值范围是( )
分析:利用等差数列的前n项和公式和配方即可得出Sn=na1+
×3=
[n-(
-
a1)]2-
(
-
a1)2,又因为S10是数列{Sn}中的唯一最小项,根据二次函数的单调性即可得出.
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:∵Sn=na1+
×3=
[n-(
-
a1)]2-
(
-
a1)2,
又∵S10是数列{Sn}中的唯一最小项,∴9.5<
-
a1<10.5,解得-30<a1<-27.
∴数列{an}的首项a1的取值范围是(-30,-27).
故选C.
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
又∵S10是数列{Sn}中的唯一最小项,∴9.5<
| 1 |
| 2 |
| 1 |
| 3 |
∴数列{an}的首项a1的取值范围是(-30,-27).
故选C.
点评:熟练掌握等差数列的前n项和公式和配方法、二次函数的单调性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=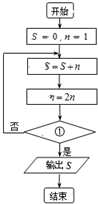 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )