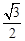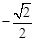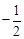题目内容
已知函数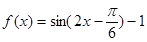 ;
;
(1)写出函数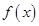 的单调递增区间;
的单调递增区间;
(2)若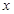
 求函数
求函数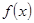 的最值及对应的
的最值及对应的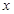 的值;
的值;
(3)若不等式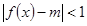 在
在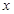
 恒成立,求实数
恒成立,求实数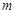 的取值范围.
的取值范围.
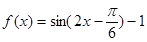 ;
; (1)写出函数
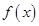 的单调递增区间;
的单调递增区间; (2)若
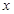
 求函数
求函数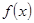 的最值及对应的
的最值及对应的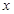 的值;
的值;(3)若不等式
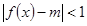 在
在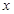
 恒成立,求实数
恒成立,求实数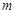 的取值范围.
的取值范围.(1)[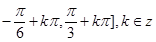 ;(2)
;(2)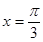 时,
时,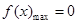 ,
,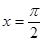 时,
时,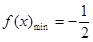 ;(1)(-1,
;(1)(-1,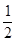 ).
).
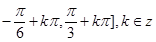 ;(2)
;(2)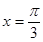 时,
时,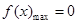 ,
,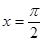 时,
时,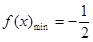 ;(1)(-1,
;(1)(-1,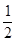 ).
).本试题主要考查了三角函数的性质的运用。
解:(1)由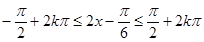 得:
得: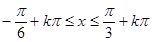
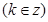 , 所以
, 所以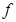 (x) 的单调递增区间为[
(x) 的单调递增区间为[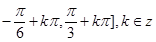 。(6分)
。(6分)
(2)由(1)知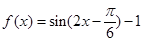 ,
,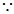 x
x ,所以
,所以 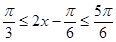
故 当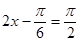 时,即
时,即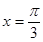 时,
时,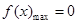 (8分)
(8分)
当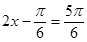 时,即
时,即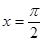 时,
时,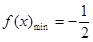 (10分)
(10分)
(3)解法1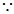
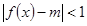
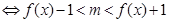 (x
(x );
);
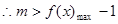 且
且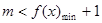 故m的范围为(-1,
故m的范围为(-1,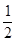 )。 (14分)
)。 (14分)
解:(1)由
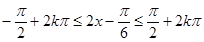 得:
得: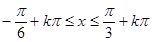
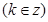 , 所以
, 所以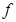 (x) 的单调递增区间为[
(x) 的单调递增区间为[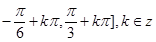 。(6分)
。(6分)(2)由(1)知
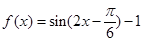 ,
,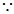 x
x ,所以
,所以 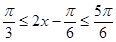
故 当
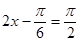 时,即
时,即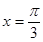 时,
时,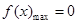 (8分)
(8分) 当
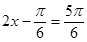 时,即
时,即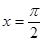 时,
时,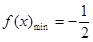 (10分)
(10分) (3)解法1
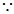
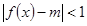
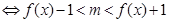 (x
(x );
);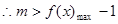 且
且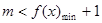 故m的范围为(-1,
故m的范围为(-1,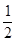 )。 (14分)
)。 (14分)
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 cos2x+
cos2x+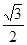 sinxcosx+1,x∈R.
sinxcosx+1,x∈R.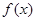 的最小正周期;
的最小正周期;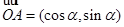 ,
, .向量
.向量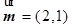 ,
,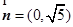 ,且
,且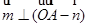 .
.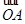 ;
;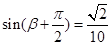 ,
,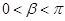 ,求
,求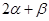 的值.
的值.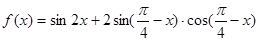
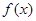 的最小正周期; (2) 求函数
的最小正周期; (2) 求函数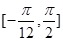 上的值域;
上的值域;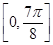 上的简图,并且依图写出函数
上的简图,并且依图写出函数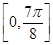 上的递增区间.
上的递增区间.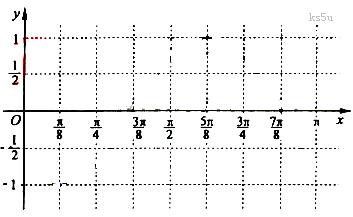
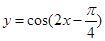 的图象,只需将函数
的图象,只需将函数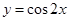 的图象( )
的图象( ) 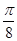 个单位
个单位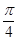 个单位
个单位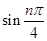 ,n∈Z,则f (1)+f (2)+f (3)+……+f(2012)=_____________.
,n∈Z,则f (1)+f (2)+f (3)+……+f(2012)=_____________. 的图象只需将y =3sin2x的图象
的图象只需将y =3sin2x的图象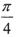 个单位
个单位 个单位
个单位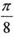 个单位
个单位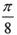 个单位
个单位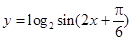 的单调递减区间是 .
的单调递减区间是 .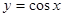 的图象上一点
的图象上一点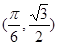 处的切线的斜率为( )
处的切线的斜率为( )