题目内容
过抛物线y2=2px(p>0)的焦点F,作直线l交抛物线于A、B两点,A、B在抛物线的准线上的射影分别是M和N,则∠MFN的大小是________.
90°
分析:根据抛物线的定义,可得△AFM是等腰三角形,底角∠MFA= (180°-∠A),同理∠NFB=
(180°-∠A),同理∠NFB= (180°-∠B).再根据平行线的同旁内角互补,得∠A+∠B=180°,从而∠MFA+∠NFB=∠90°,得到∠MFN的大小为90°.
(180°-∠B).再根据平行线的同旁内角互补,得∠A+∠B=180°,从而∠MFA+∠NFB=∠90°,得到∠MFN的大小为90°.
解答:∵点A在抛物线y2=2px上,F为抛物线的焦点,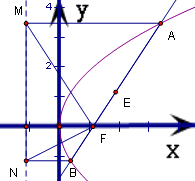
AM是A到抛物线准线的距离
∴△AFM中,AM=AF,可得∠FMA=∠MFA= (180°-∠A)
(180°-∠A)
同理可得:∠FNB=∠NFB= (180°-∠B)
(180°-∠B)
∴∠MFA+∠NFB= (360°-∠A-∠B)
(360°-∠A-∠B)
∵AM∥BN
∴∠A+∠B=180°,得∠MFA+∠NFB=∠90°;
由此可得∠MFN=180°-(∠MFA+∠NFB)=∠90°
故答案为:90°
点评:本题给出抛物线过焦点的弦在准线上的射影,求射影点对焦点的张角的大小,着重考查了用平面几何理解抛物线的定义的知识点,属于基础題.
分析:根据抛物线的定义,可得△AFM是等腰三角形,底角∠MFA=
 (180°-∠A),同理∠NFB=
(180°-∠A),同理∠NFB= (180°-∠B).再根据平行线的同旁内角互补,得∠A+∠B=180°,从而∠MFA+∠NFB=∠90°,得到∠MFN的大小为90°.
(180°-∠B).再根据平行线的同旁内角互补,得∠A+∠B=180°,从而∠MFA+∠NFB=∠90°,得到∠MFN的大小为90°.解答:∵点A在抛物线y2=2px上,F为抛物线的焦点,

AM是A到抛物线准线的距离
∴△AFM中,AM=AF,可得∠FMA=∠MFA=
 (180°-∠A)
(180°-∠A)同理可得:∠FNB=∠NFB=
 (180°-∠B)
(180°-∠B)∴∠MFA+∠NFB=
 (360°-∠A-∠B)
(360°-∠A-∠B)∵AM∥BN
∴∠A+∠B=180°,得∠MFA+∠NFB=∠90°;
由此可得∠MFN=180°-(∠MFA+∠NFB)=∠90°
故答案为:90°
点评:本题给出抛物线过焦点的弦在准线上的射影,求射影点对焦点的张角的大小,着重考查了用平面几何理解抛物线的定义的知识点,属于基础題.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
=
,
•
=48,则抛物线的方程为( )
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为抛物线的顶点.则△ABO是一个( )
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |