题目内容
【题目】某商家在某一天统计前5名顾客扫微信红包所得金额分别为5.9元,5.7元,4.7元,3.3元,2.1元,商家从这5名顾客中随机抽取3人赠送礼品.
(Ⅰ)求获得礼品的3人中恰好有2人的红包超过5元的概率;
(Ⅱ)商家统计一周内每天使用微信支付的人数![]() 与每天的净利润
与每天的净利润![]() (单位:元),得到如下表:
(单位:元),得到如下表:
| 12 | 16 | 22 | 25 | 26 | 29 | 30 |
| 60 | 100 | 210 | 240 | 150 | 270 | 330 |
根据表中数据用最小二乘法求![]() 与
与![]() 的回归方程
的回归方程![]() (
(![]() ,
,![]() 的计算结果精确到小数点后第二位)并估计使用微信支付的人数增加到36人时,商家当天的净利润为多少(计算结果精确到小数点后第二位)?
的计算结果精确到小数点后第二位)并估计使用微信支付的人数增加到36人时,商家当天的净利润为多少(计算结果精确到小数点后第二位)?
参考数据及公式:
①![]() ,
,![]() ;
;![]() ;
;![]()
②回归方程:![]() (其中
(其中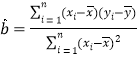 ,
,![]() )
)
【答案】(Ⅰ)![]() ;(Ⅱ)364.58元
;(Ⅱ)364.58元
【解析】
(Ⅰ)利用古典概型的概率公式求获得礼品的3人中恰好有2人的红包超过5元的概率;(Ⅱ)利用最小二乘法求![]() 与
与![]() 的回归方程为
的回归方程为![]() ,把
,把![]() 代入方程,即可得解.
代入方程,即可得解.
(Ⅰ)记“5名顾客扫微信红包所得金额超过5元的2人”为![]() ,
,![]() ,“不超过5元的3人”为
,“不超过5元的3人”为![]() ,
,![]() ,
,![]() ,“获得礼品的3人中恰好有2人的红包超过5元”为事件
,“获得礼品的3人中恰好有2人的红包超过5元”为事件![]() ,
,
则所有的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种,
共10种,
其中事件![]() 包含的基本事件有
包含的基本事件有![]() ,
,![]() ,
,![]() 共3种,
共3种,
所以![]() .
.
(Ⅱ)∵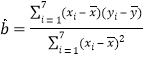
![]() ,
,
∴![]() .
.
所以![]() 与
与![]() 的回归方程为
的回归方程为![]() ,
,
当![]() 时,
时,![]() .
.
故估计使用微信支付的人数增加到36人时,商家当天的净利润约为364.58元.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号x | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款y(千亿元) | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于x的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数r的平方,当
恰好等于相关系数r的平方,当![]() 时,认为线性冋归模型是有效的,请计算
时,认为线性冋归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到0.001).
并且评价模型的拟合效果(计算结果精确到0.001).
附:
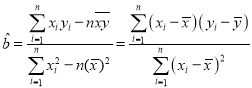 ,
,
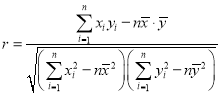
![]()

