题目内容
由曲线y=sin(
x)与y=x3在区间[0,1]上所围成的图形面积为
-
-
.
| π |
| 2 |
| 2 |
| π |
| 1 |
| 4 |
| 2 |
| π |
| 1 |
| 4 |
分析:作出两曲线在第一象限的图象如图,可得它们的公共点恰好为原点和A(1,1).接下来根据定积分公式求出函数sin(
x)-x3在区间[0,1]上积分的值,即为所求图形的面积.
| π |
| 2 |
解答:解:曲线y=sin(
x)与y=x3在原点处相交,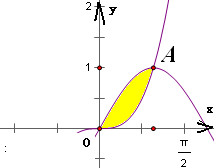
且在第一象限内交于点A(1,1)
因此,所求阴影部分面积为
S=
(sin(
x)-x3)dx=(-
cos
x-
x4+C)
,(其中C是常数)
=(-
cos
-
×14+C)-(-
cos0-
×04+C)=
-
故答案为:
-
| π |
| 2 |

且在第一象限内交于点A(1,1)
因此,所求阴影部分面积为
S=
| ∫ | 1 0 |
| π |
| 2 |
| 2 |
| π |
| π |
| 2 |
| 1 |
| 4 |
| | | 1 0 |
=(-
| 2 |
| π |
| π |
| 2 |
| 1 |
| 4 |
| 2 |
| π |
| 1 |
| 4 |
| 2 |
| π |
| 1 |
| 4 |
故答案为:
| 2 |
| π |
| 1 |
| 4 |
点评:本题根据两个曲线方程,求它们在在区间[0,1]上所围成的图形面积.考查了定积分的计算公式和定积分的几何意义等知识,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
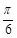 )的图像可由曲线y=1+cos2x向左平移
)的图像可由曲线y=1+cos2x向左平移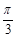 个单位得到;②函数y=sin(x+
个单位得到;②函数y=sin(x+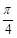 )+cos(x+
)+cos(x+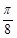 是曲线y=sin(2x+
是曲线y=sin(2x+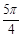 )的一条对称轴;④函数y=2sin2(x+
)的一条对称轴;④函数y=2sin2(x+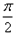 x)与y=x3在区间[0,1]上所围成的图形面积为( )。
x)与y=x3在区间[0,1]上所围成的图形面积为( )。