Question

【题目】在直三棱柱ABC﹣A1B1C1中，AB⊥BC，BB1BC，D是CC1的中点．

（1）证明：B1C⊥平面ABD；

（2）若AB＝BC，E是A1C1的中点，求二面角A﹣BD﹣E的大小．

Answer 1

【答案】（1）详见解析；（2）60°．

【解析】

（1）设BC＝2，证明△DCB∽△CBB1，得∠BDC＝∠BCB1，可得∠DBC+∠BCB1＝90°，则BD⊥B1C，由三棱柱ABC﹣A1B1C1是直三棱柱，得BB1⊥AB，进一步得到AB⊥平面BCC1B1，从而有AB⊥B1C，进一步得到B1C⊥平面ABD；

（2）设BC＝2，以B为坐标原点建立空间直角坐标系，分别求出平面ABD的一个法向量与平面BDE的一个法向量，由两法向量所成角的余弦值可得二面角A﹣BD﹣E的大小．

（1）设BC＝2，

∴，，．

∴，则△DCB∽△CBB1，得∠BDC＝∠BCB1，

∵∠DBC+∠BDC＝90°，

∴∠DBC+∠BCB1＝90°，

得BD⊥B1C．

∵三棱柱ABC﹣A1B1C1是直三棱柱，

∴BB1⊥平面ABC，

又AB平面ABC，

∴BB1⊥AB，

又∵AB⊥BC，BB1∩BC＝B，

∴AB⊥平面BCC1B1，

而B1C平面BCC1B1，

∴AB⊥B1C，

又BD∩AB＝B，

∴B1C⊥平面ABD；

（2）解：设BC＝2，建立如图所示空间直角坐标系，

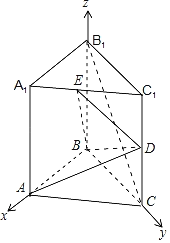
由（1）知，E（1，1，2），D（0，2，），

A（2，0，0），B1（0，0，），C（0，2，0）．

由（1）知平面ABD的一个法向量，

，．

设平面BDE的一个法向量为．

由，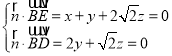

取z，得．

∴cos．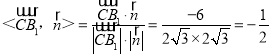

由图可知二面角A﹣BD﹣E为锐角，

则二面角A﹣BD﹣E的大小为60°．