题目内容
【题目】如图，直四棱柱ABCD﹣A1B1C1D1的底面ABCD是直角梯形，其中AB⊥AD，AB=2AD=2AA1=4，CD=1．
（Ⅰ）证明：BD1⊥平面A1C1D；
（Ⅱ）求BD1与平面A1BC1所成角的正弦值．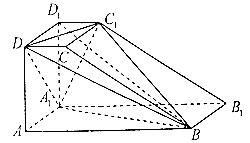
【答案】（Ⅰ）证明：连接AD1 ， B1D1 ， 则AB是平面AD1的垂线，BD1是平面AD1的斜线，AD1是BD1在平面AD1内的射影，∴A1D⊥BD1 ， ∵Rt△C1D1A1∽Rt△B1A1D1 ， ∴∠D1A1C1+∠A1D1B1=∠D1A1C1+∠D1C1A1=90°，∴A1C1⊥B1D1 ， ∴A1C1⊥BD1 ，
∵A1D∩A1C1=A1 ，
∴BD1⊥平面A1C1D；
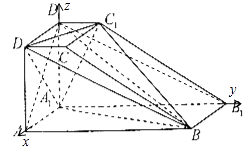
（Ⅱ）解：建立如图所示的坐标系，则A1（0，0，0），B（2，4，0），C1（0，1，2），D1（0，0，2），
=（2，4，0）， 
=（0，1，2）， 
=（﹣2，﹣4，2），
设BD1与平面A1BC1所成角为θ，平面A1BC1的一个法向量为 
=（x，y，z），则 
，取 =（4，﹣2，1），
则sinθ=| 
= 
．
【解析】（Ⅰ）连接AD1 ， B1D1 ， 证明A1D⊥BD1 ， A1C1⊥BD1 ， 即可证明：BD1⊥平面A1C1D；（Ⅱ）建立坐标系，求出平面的法向量，即可求BD1与平面A1BC1所成角的正弦值．
【考点精析】本题主要考查了直线与平面垂直的判定和空间角的异面直线所成的角的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则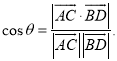
才能正确解答此题．
