题目内容
【题目】如图，从椭圆 
上一点P向x轴作垂线，垂足恰为左焦点F1 ， 又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且 
． （Ⅰ） 求椭圆的方程；
（Ⅱ） 若M是椭圆上的动点，点N（4，2），求线段MN中点Q的轨迹方程．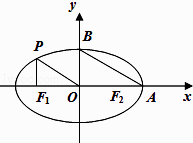
【答案】解：（Ⅰ） 由题意可知，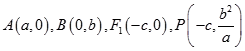 
，∵AB∥OP，
∴kAB=kOP ，
∴ 
，
∵a2=b2+c2 ，
∴a2=2c2 ，
∴ 
，
∴ 
， 
，
∴ 
， 
， 
，
∴椭圆方程为 
．
（Ⅱ） 设Q（x，y），已知点Q为线段MN中点，N（4，2），则M（2x﹣4，2y﹣2），
∵M是椭圆 上的动点，
∴ 
，
即 
．
【解析】（Ⅰ） 由题意可知：求得A，B，F1 ， P点坐标，由kAB=kOP ， 根据斜率公式，求得b和c的值，根据椭圆的性质， 
，由 
，即可求得a和b的值，求得椭圆方程；（Ⅱ） 由题意可知：根据中点坐标公式，求得M点坐标，将M代入椭圆方程，即可求得Q的轨迹方程．
练习册系列答案
相关题目
【题目】已知函数f（x）=2x+2ax（a为实数），且f（1）= 
．
（1）求函数f（x）的解析式；
（2）判断函数f（x）的奇偶性并证明；
（3）判断函数f（x）在区间[0，+∞）的单调性，并用定义证明．
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin（ωx+φ） | 0 | 2 | ﹣2 | 0 |
（1）请将上表数据补充完整，并直接写出函数f（x）的解析式；
（2）将函数y=f（x）的图象向左平移 
个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）的单调递减区间．
