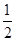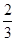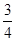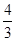题目内容
已知点A(-
,0)和B(
,0),动点C与A、B两点的距离之差的绝对值为2,点C的轨迹与直线y=x-2交于D、E两点,求线段DE的长.
| 3 |
| 3 |
设点C(x,y),则|CA|-|CB|=±2.
根据双曲线的定义,可知点C的轨迹是双曲线
-
=1.
由2a=2,2c=|AB|=2
,得a2=1,b2=2.
故点C的轨迹方程是x2-
=1.
由
,得 x2+4x-6=0.
∵△>0,∴直线与双曲线有两个交点.
设D(x1,y1)、E(x2,y2),则 x1+x2=-4,x1•x2=-6.
故|DE|=
=
=4
.
根据双曲线的定义,可知点C的轨迹是双曲线
| x2 |
| a2 |
| y2 |
| b2 |
由2a=2,2c=|AB|=2
| 3 |
故点C的轨迹方程是x2-
| y2 |
| 2 |
由
|
∵△>0,∴直线与双曲线有两个交点.
设D(x1,y1)、E(x2,y2),则 x1+x2=-4,x1•x2=-6.
故|DE|=
| (x1-x2)2+(y1-y2)2 |
| 2 |
| (x1+x2)2-4x1x2 |
| 5 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
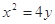 ,过点
,过点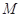
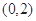 作直线与抛物线交于两点
作直线与抛物线交于两点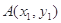 ,
,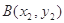 ,过
,过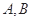 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为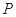 .
.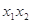 的值;
的值;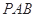 面积的最小值.
面积的最小值.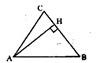
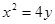 的焦点是( )
的焦点是( )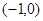
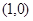
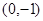
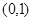
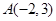 在抛物线C:
在抛物线C: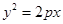 的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )
的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为( )