题目内容
自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表所示.
经调查发现,堵车概率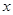 在
在 上变化,
上变化, 在
在 上变化.
上变化.
在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
(1)求 段平均堵车时间
段平均堵车时间 的值;
的值;
(2)若只考虑所花汽油费的期望值大小,为了节约,求选择走甲线路的概率.
| | CD段 | EF段 | GH段 |
| 堵车概率 | 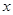 |  |  |
| 平均堵车时间 (单位:小时) |  | 2 | 1 |
经调查发现,堵车概率
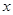 在
在 上变化,
上变化, 在
在 上变化.
上变化.在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计
 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1, 2] | 6 |
| (2, 3] | 38 |
| (3, 4] | 24 |
| (4, 5] | 24 |
(1)求
 段平均堵车时间
段平均堵车时间 的值;
的值;(2)若只考虑所花汽油费的期望值大小,为了节约,求选择走甲线路的概率.
(1)3;(2)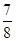 .
.
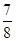 .
.试题分析:本题考查利用频率分布表求平均数,相互独立事件同时发生的概率,离散型随机变量分布列,数学期望,几何概型等基础知识;考查运用统计、概率、数学期望等数学知识解决实际问题的能力,以及运算求解能力;考查数形结合数学思想方法.第一问,用总的堵车时间除以总人数100人,即得到平均堵车时间;第二问,利用独立事件求出每种情况的概率,选择甲路线说明甲需汽油费少,利用线性规划化画出区域图,再利用几何概型求概率;法二,分别求EF路段和GH路段的期望再相加求乙路线多花汽油费的期望.
试题解析:(1)
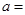
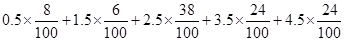 2分
2分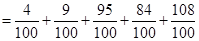
 3. 4分
3. 4分(2)设走甲线路所花汽油费为
 元,
元,则
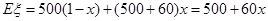 . 5分
. 5分法一:设走乙线路多花的汽油费为
 元,∵
元,∵ 段与
段与 段堵车与否相互独立,
段堵车与否相互独立,∴
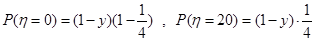 ,
, , 7分
, 7分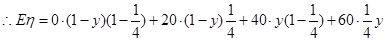
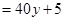 . 8分
. 8分∴走乙线路所花的汽油费的数学期望为
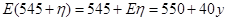 . 9分
. 9分依题意,选择走甲线路应满足
 , 10分
, 10分即
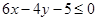 ,又
,又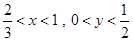 ,
,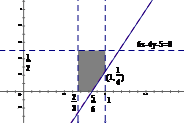
 (选择走甲线路)
(选择走甲线路)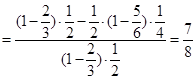 . 13分
. 13分法二:在EF路段多花汽油费的数学期望是
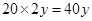 元, 6分
元, 6分在GH路段多花汽油费的数学期望是
 元, 7分
元, 7分因为EF、GH路段堵车与否相互独立,
所以走乙路线多花汽油费的数学期望是
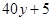 元. 8分
元. 8分以下解法同法一.

练习册系列答案
相关题目
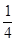 B.
B.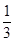 C.
C.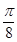 D.
D.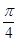
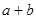 <
< 的概率为 .
的概率为 .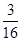 ,则a的值为( )
,则a的值为( )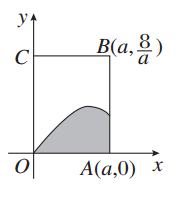
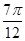
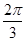
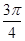
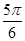
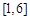 上随机取一个实数
上随机取一个实数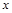 ,使得
,使得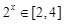 的概率为( )
的概率为( )


