题目内容
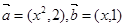
(1)若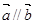 ,求
,求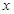 ;
;
(2)若函数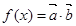 对应的图象记为
对应的图象记为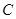
(3)求曲线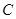 在
在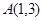 处的切线方程?(II)若直线
处的切线方程?(II)若直线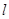 为曲线
为曲线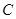 的切线,并且直线
的切线,并且直线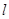 与曲线
与曲线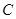 有且仅有一个公共点,求所有这样直线
有且仅有一个公共点,求所有这样直线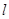 的方程?
的方程?
【答案】
(1)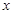 =2或0(2)
=2或0(2)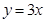 (3)y=2
(3)y=2
【解析】本试题主要是考查了向量的共线,以及曲线的切线方承担求解,直线与曲线的交点问题的综合运用
(1)由于向量共线,那么根据坐标关系式得到参数x的值。
(2)由于函数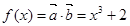 则由
则由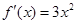
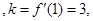 得到切线方程。
得到切线方程。
设切点坐标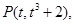
曲线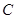 在
在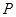 处的切线方程为
处的切线方程为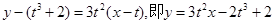 ,然后联立方程组,得到参数t的值。
,然后联立方程组,得到参数t的值。
解:
(1)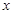 =2或0………3分; [
=2或0………3分; [ 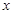 =2给两分]
=2给两分]
(2)函数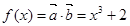 ………4分
………4分
(I)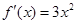
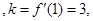 ………6分
………6分
曲线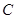 在
在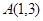 处的切线方程为
处的切线方程为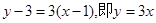 ………7分
………7分
(II)设切点坐标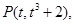 ………8分
………8分
曲线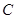 在
在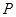 处的切线方程为
处的切线方程为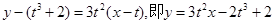 ………9分
………9分
由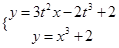 得
得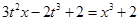 即
即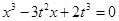 ………10分
………10分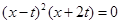
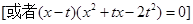 ………12分
………12分
由题意得t=0………13分
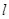 的方程为y=2………14分
的方程为y=2………14分

练习册系列答案
相关题目
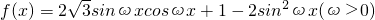 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.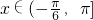 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间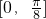 上的最小值.
上的最小值.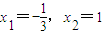 ,求函数f(x)的解析式;
,求函数f(x)的解析式; ,求b的最大值.
,求b的最大值.