题目内容
(14分)已知数列 满足
满足 ,
,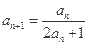 ,
,
(Ⅰ)计算出 、
、 、
、 ;
;
(Ⅱ)猜想数列 通项公式
通项公式
 ,并
,并 用数学归纳法进行证明.
用数学归纳法进行证明.
 满足
满足 ,
,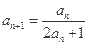 ,
,(Ⅰ)计算出
 、
、 、
、 ;
;(Ⅱ)猜想数列
 通项公式
通项公式
 ,并
,并 用数学归纳法进行证明.
用数学归纳法进行证明.(Ⅰ)


 -------------------------3分;
-------------------------3分;
(Ⅱ)由⑴知 分子是3,分母是以首项为5公
分子是3,分母是以首项为5公 差为6的等差数列
差为6的等差数列
∴猜想数列 通项公式:
通项公式: ---------------------6分
---------------------6分
用数学归纳法证明如下:
(1)当 时,由题意可知
时,由题意可知 ,命题成立.
,命题成立.
(2)假设当
 时命题成立,即
时命题成立,即 ,----8分
,----8分
那么,当 时,
时,
也就说,当 时命题也成立----------------------------------------------13分
时命题也成立----------------------------------------------13分
综上所述,数列 的通项公式为
的通项公式为 ---------------------------14分
---------------------------14分



 -------------------------3分;
-------------------------3分;(Ⅱ)由⑴知
 分子是3,分母是以首项为5公
分子是3,分母是以首项为5公 差为6的等差数列
差为6的等差数列∴猜想数列
 通项公式:
通项公式: ---------------------6分
---------------------6分用数学归纳法证明如下:
(1)当
 时,由题意可知
时,由题意可知 ,命题成立.
,命题成立.
(2)假设当

 时命题成立,即
时命题成立,即 ,----8分
,----8分那么,当
 时,
时,
也就说,当
 时命题也成立----------------------------------------------13分
时命题也成立----------------------------------------------13分综上所述,数列
 的通项公式为
的通项公式为 ---------------------------14分
---------------------------14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,
, ,则公差等于( )
,则公差等于( )
 中的
中的 (12分)
(12分) 中,Sn为
中,Sn为 项和,已知
项和,已知 ,则
,则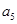 等于 ( )
等于 ( ) 


 中,若
中,若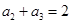 ,
, ,则
,则 ( )
( )



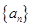 中,
中,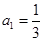 ,
,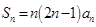 ,通过求
,通过求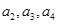 ,猜想
,猜想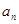 的表达式为( )
的表达式为( )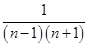



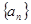 满足
满足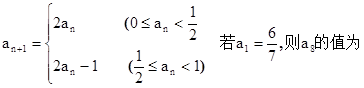 ( )
( )



 次
次
 中,
中, ,
, ,则
,则 ( )
( )