题目内容
如图所示,已知函数y=ax+b和y=ax2+bx+c(a≠0),则它们的图象可能是( )
思路解析:这是一道考查阅读图象能力的考题.一次函数和二次函数图象的组合,实质上是考查两个函数的系数之间的联系,因此分类进行讨论即可得到正确答案.另外,要从图象中获取有价值的信息——即将图象反映出来的性质用符号语言表示出来,如从图象中可以看出一次函数是单调递增的,则a>0.就是非常重要的已知条件.
解法一:(分类讨论法)∵决定函数图象位置和趋势的因素主要是a和b,其中二次函数的对称轴的符号是解答此类考题的至关重要的因素,∴分四种情况进行讨论①![]() ②
②![]() ③
③![]() ④
④![]() 对称轴为x=-
对称轴为x=-![]() .因此,B正确.
.因此,B正确.
解法二:(排除法)从图象可知函数y=ax+b是单调递增的,
∴a>0,排除C和D.
又∵二次函数的对称轴不是y轴,
∴b≠0,排除A.因此,选B.
解法三:(特征值法)∵题中的待定系数具有任意性,不妨令a=b=1,则B符合要求,因此,选B.
答案:B

练习册系列答案
相关题目
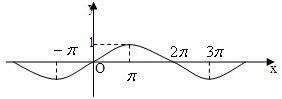 已知函数y=sinωx(ω>0)在一个周期内的图象如图所示,要得到函数y=sin(
已知函数y=sinωx(ω>0)在一个周期内的图象如图所示,要得到函数y=sin(| 1 |
| 2 |
| π |
| 12 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
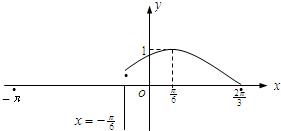 已知定义在区间
已知定义在区间 如图所示,已知一次函数y=kx+b(b>0)与二次函数
如图所示,已知一次函数y=kx+b(b>0)与二次函数 为了预防流感,某学校对教室用药熏消毒法进行消毒.如图所示,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,室内每立方米空气中的含药量y(毫克)与时间t(小时)的函数关系式为
为了预防流感,某学校对教室用药熏消毒法进行消毒.如图所示,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,室内每立方米空气中的含药量y(毫克)与时间t(小时)的函数关系式为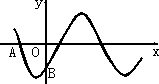
 时,方程f(x)=2a恒有解,求实数a的取值范围.
时,方程f(x)=2a恒有解,求实数a的取值范围.