题目内容
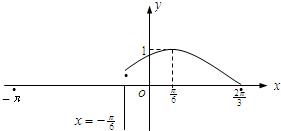 已知定义在区间[-π,
已知定义在区间[-π,| 2 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
(Ⅰ)求函数y=f(x)在[-π,
| 2 |
| 3 |
(Ⅱ)求方程f(x)=
| ||
| 2 |
(Ⅲ)是否存在常数m的值,使得|f(x)-m|<2在x∈[-π,
| 2π |
| 3 |
值范围;若不存在,请说明理由.
分析:(Ⅰ)根据图象中函数值的最大值判断出A的值,利用函数图象与x轴的交点判断出函数的周期,进而求得ω,把点(
,1)代入求得φ的值,则当x∈[ -
,
π ]时,函数的解析式可得;进而利用函数图象关于直线x=-
对称利用f(x)=f(-x-
)求得[-π,
]的函数解析式,最后综合答案可得.
(Ⅱ)分别看-
≤x≤
和-π≤x<-
利用(Ⅰ)中函数的解析式,求得x的值.
(Ⅲ)问题可转化为m-2<f(x)<m+2在x∈[-π,
]上恒成立,联立方程组利用三角函数的性质求得m的范围.
| π |
| 6 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
(Ⅱ)分别看-
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
(Ⅲ)问题可转化为m-2<f(x)<m+2在x∈[-π,
| 2π |
| 3 |
解答:解:(Ⅰ)x∈[-
,
π],A=1,
=
-
,T=2π,ω=1
且f(x)=sin(x+φ)过(
,1),
∵-
<?<
∴
+φ=
,φ=
,f(x)=sin(x+
)
当-π≤x<-
时,-
≤-x-
≤
,f(-x-
)=sin(-x-
+
)
而函数y=f(x)的图象关于直线x=-
对称,则f(x)=f(-x-
)
即f(x)=sin(-x-
+
)=-sinx,-π≤x<-
∴f(x)=
(Ⅱ)当-
≤x≤
时,
≤x+
≤π,f(x)=sin(x+
)=
x+
=
,或
,x=-
,或
当-π≤x<-
时,f(x)=-sinx=
,sinx=-
x=-
,或-
∴x=-
,-
,-
,或
为所求.
(Ⅲ)由条件得:m-2<f(x)<m+2在x∈[-π,
]上恒成立即
,由图象可得:
∴-1<m<2
| π |
| 6 |
| 2 |
| 3 |
| T |
| 4 |
| 2π |
| 3 |
| π |
| 6 |
且f(x)=sin(x+φ)过(
| π |
| 6 |
∵-
| π |
| 2 |
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
当-π≤x<-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
而函数y=f(x)的图象关于直线x=-
| π |
| 6 |
| π |
| 3 |
即f(x)=sin(-x-
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
∴f(x)=
|
(Ⅱ)当-
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 12 |
| 5π |
| 12 |
当-π≤x<-
| π |
| 6 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴x=-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 12 |
| 5π |
| 12 |
(Ⅲ)由条件得:m-2<f(x)<m+2在x∈[-π,
| 2π |
| 3 |
|
|
∴-1<m<2
点评:本题主要考查了利用y=Asin(ωx+∅)的部分图象确定函数的解析式.充分利用了三角函数的定义域,值域,对称性,周期性等性质.

练习册系列答案
相关题目
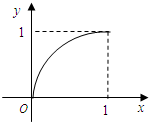 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: