题目内容
已知P是△ABC所在平面α外一点，且PA=PB=PC，则P在α上的射影一定是△ABC的（ ）A．内心
B．外心
C．重心
D．垂心
【答案】分析：点P在平面ABC上的射为O，利用已知条件，证明OA=OB=OC，推出结论．
解答：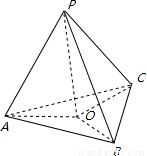
解：设点P作平面ABC的射影O，由题意：PA=PB=PC，因为PO⊥底面ABC，
所以△PAO≌△POB≌△POC
即：OA=OB=OC
所以O为三角形的外心．
故选B．
点评：本题考查棱锥的结构特征，考查逻辑思维能力，是基础题．
解答：
解：设点P作平面ABC的射影O，由题意：PA=PB=PC，因为PO⊥底面ABC，所以△PAO≌△POB≌△POC
即：OA=OB=OC
所以O为三角形的外心．
故选B．
点评：本题考查棱锥的结构特征，考查逻辑思维能力，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知P是△ABC所在平面内一点，
+
+2
=
，现将一粒黄豆随机撒在△ABC内，则黄豆落在△APC内的概率是（ ）
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P是△ABC所在平面内的一点，若
-
=λ
，其中λ∈R，则点P一定在（ ）
| CB |
| PB |
| PA |
| A、AC边所在的直线上 |
| B、BC边所在的直线上 |
| C、AB边所在的直线上 |
| D、△ABC的内部 |