题目内容
（选做题）设实数x，y，z满足x+2y-3z=7，求x2+y2+z2的最小值．
【答案】分析：利用柯本不等式，可得（x2+y2+z2）[12+22+（-3）2]≥（x+2y-3z）2，结合已知等式和不等式等号成立的条件，不难得出x2+y2+z2的最小值及其相应的x、y、z值．
解答：解：由柯西不等式，得（x2+y2+z2）[12+22+（-3）2]≥（x+2y-3z）2，
∵x+2y-3z=7，
∴14（x2+y2+z2）≥49，得x2+y2+z2≥
当且仅当x=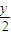
=
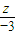时，即x=
，y=1，z=-
时，x2+y2+z2的最小值为
．
点评：本题给出条件等式，求x2+y2+z2的最小值，着重考查了利用柯西不等式求最值的知识，属于基础题．
解答：解：由柯西不等式，得（x2+y2+z2）[12+22+（-3）2]≥（x+2y-3z）2，
∵x+2y-3z=7，
∴14（x2+y2+z2）≥49，得x2+y2+z2≥
当且仅当x=
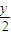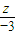=时，即x=，y=1，z=-时，x2+y2+z2的最小值为．点评：本题给出条件等式，求x2+y2+z2的最小值，着重考查了利用柯西不等式求最值的知识，属于基础题．
练习册系列答案
相关题目
A．（不等式选做题）若关于x的不等式|x+3|-|x+2|≥log2a有解，则实数a的取值范围是：
（考生注意：只能从下列A、B、C三题中选做一题，如果多做，则按第一题评阅记分）