题目内容
【题目】已知右焦点为
的椭圆
（
）过点
，且椭圆
关于
直线
对称的图形过坐标原点.
（1）求椭圆的方程；
（2）过点
作直线
与椭圆交于点
(异于椭圆的左、右顶点)，线段
的中点为
.点
是椭圆的右顶点.求直线
的斜率
的取值范围.
【答案】(1)
；(2)
.
【解析】试题分析：
（1）由椭圆
过点
可得
，有椭圆关于直线
对称的图形过坐标原点可得
，据此可得椭圆方程为.
（2）设椭圆的y轴截距方程为
，联立直线方程与椭圆方程可得
，则
，
，
，分类讨论：①当
时，
；②当
时，
，由均值不等式的结论可得
，且
.据此可得
的取值范围是
.
试题解析：
（1）∵椭圆过点.
∴，①
∵椭圆关于直线对称的图形过坐标原点，
∴，
∴
，②
由①②得
，
，
∴椭圆的方程为.
（2）依题意，直线
过点
，且斜率不为零，
∴可设其方程为.
联立方程组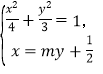
消去
并整理，
得.
设
，
，
，
则
.
∴，，∴.
①当时，；
②当时，，
∵
，∴
，
∴，且.
综合①②，可知直线
的斜率的取值范围是.
练习册系列答案
名校课堂系列答案
相关题目
【题目】某学校900名学生在一次百米测试中，成绩全部介于13秒与18 秒之间，利用分层抽样的方法抽取其中若干个样本，将测试结果按如下方式分成五组：第一组[13,14），第二组[14,15），…，第五组[17,18]，有关数据见下表：
各组组员数 | 各组抽取人数 | |
[13,14） | 54 | a |
[14,15） | b | 8 |
[15,16） | 342 | 19 |
[16,17） | 288 | c |
[17,18] | d |
（1）求a,b,c,d的值；
（2）若样本第一组中只有一个女生，其他都是男生，第五组则只有一个男生，其他都是女生，现从第一、五组中各抽一个同学组成一个新的组，求这个新组恰好由一个男生和一个女生构成的概率。
