题目内容
已知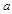 为实数,
为实数,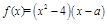 ,
,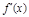 为
为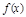 的导函数.
的导函数.
(Ⅰ)若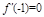 ,求
,求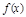 在
在 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若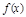 在
在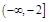 和
和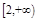 上均单调递增,求
上均单调递增,求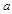 的取值范围
的取值范围
【答案】
(Ⅰ) 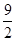 ,
,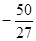 (Ⅱ)
(Ⅱ) 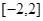
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)根据导数的符号与函数单调性的关系得到函数的极值,进而得到最值。
(2)因为函数给定区间是单调的,则必有导数恒大于等于零或者恒小于等于零,得到参数的范围。
解:(1)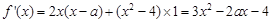 .
.
(2)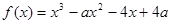 ,
,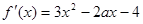 .
.
由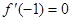 ,得
,得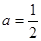 ,此时
,此时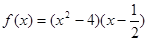 ,
,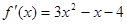 ,
,
由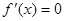 ,得
,得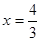 或
或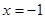 .
.
又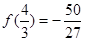 ,
,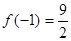 ,
,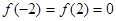 ,
,
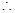
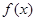 在
在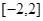 上的最大值为
上的最大值为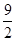 ,最小值为
,最小值为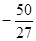 .
.
(3)解法一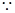
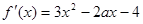 ,
,
依题意: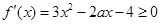 对
对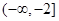 恒成立,即
恒成立,即
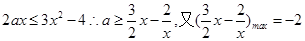 ,所以
,所以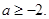
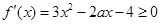 对
对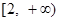 恒成立,即
恒成立,即
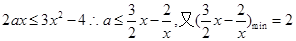 ,所以
,所以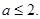
综上: 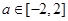 .
.
解法二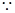
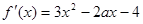 ,
,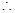
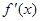 的图像是开口向上且过点
的图像是开口向上且过点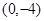 的抛物线,由条件得
的抛物线,由条件得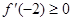 ,
,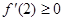 ,
,
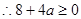 ,
,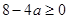 .解得
.解得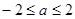 .
. 
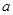 的取值范围为
的取值范围为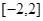 .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
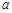 为实数,
为实数, ,
,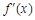 为
为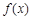 的导函数.
的导函数. ;
;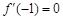 ,求
,求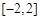 上的最大值和最小值;
上的最大值和最小值;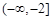 和
和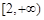 上都是递增的,求
上都是递增的,求 x2,g(x)=logax(a>0且a≠1),h(x)=f(x)-g(x)在定义域上为减函数,且其导函数h′(x)存在零点.
x2,g(x)=logax(a>0且a≠1),h(x)=f(x)-g(x)在定义域上为减函数,且其导函数h′(x)存在零点. ,判断P(x0),,P(x1),P(x2)的大小,并证明你的结论.
,判断P(x0),,P(x1),P(x2)的大小,并证明你的结论.