题目内容
7.函数y=-x2+|x|,单调递减区间为[$-\frac{1}{2}$,0),[$\frac{1}{2}$,+∞),最大值和最小值的情况为最大值为$\frac{1}{4}$,无最小值.分析 去绝对值号便得到$y=\left\{\begin{array}{l}{-{x}^{2}+x}&{x≥0}\\{-{x}^{2}-x}&{x<0}\end{array}\right.$,这样根据二次函数的单调区间的求法,求出每段上的单调减区间即可,可判断该函数在整个定义域上的单调性,根据单调性即可画出该函数的草图,根据图象即可判断其最大值和最小值情况.
解答 解:$y=-{x}^{2}+|x|=\left\{\begin{array}{l}{-{x}^{2}+x}&{x≥0}\\{-{x}^{2}-x}&{x<0}\end{array}\right.$;
∴x≥0时,该函数在$[\frac{1}{2},+∞)$上单调递减;
x<0时,该函数在$[-\frac{1}{2},0)$上单调递减;
∴该函数的单调递减区间为:[$-\frac{1}{2}$,0),[$\frac{1}{2},+∞$);
该函数在(-∞,$-\frac{1}{2}$)上单调递增,在[$-\frac{1}{2},0$)上单调递减,在[0,$\frac{1}{2}$)上单调递增,在[$\frac{1}{2}$,+∞)上单调递减;
且x=$-\frac{1}{2}$时,y=$\frac{1}{4}$,x=$\frac{1}{2}$时,y=$\frac{1}{4}$;
∴该函数有最大值$\frac{1}{4}$,无最小值.
故答案为:$[-\frac{1}{2},0),[\frac{1}{2},+∞)$,有最大值$\frac{1}{4}$,无最小值.
点评 考查含绝对值函数的处理方法:去绝对值号,以及分段函数单调区间的求法,二次函数的单调性及单调区间的求法,根据函数的单调性求函数最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知等差数列的首项a1=2,公差d=-2,前n项的和Sn=-70,则n=( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
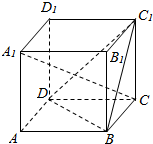 棱长为1的正方体AC1中,求证:A1C⊥平面BDC1.
棱长为1的正方体AC1中,求证:A1C⊥平面BDC1.