题目内容
下列函数中，在区间（1，+∞）上是增函数的是（ ）
| A、y=-x+1 | ||
| B、y=31-x | ||
| C、y=-（x-1）2 | ||
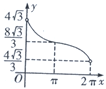
D、y=
|
考点：函数单调性的判断与证明
专题：数形结合,函数的性质及应用
分析：此题涉及到的函数比较简单，所以可采用图象法判断．
解答：解：图象法：结合图象易知A、B选项不符合题意；
对于选项B，函数y=31-x可化为y=(
)x-1，所以其图象是由y=(
)x的图象向右平移1个单位得到，
所以y=31-x在[1，+∞）上是减函数．
故选D
另外函数y=
=
，可看作是将y=-
的图象沿x轴向右平移1个单位得到的，所以该函数在[1，+∞）上是增函数．
故选D
对于选项B，函数y=31-x可化为y=(
| 1 |
| 3 |
| 1 |
| 3 |
所以y=31-x在[1，+∞）上是减函数．
故选D
另外函数y=
| 1 |
| 1-x |
| -1 |
| x-1 |
| 1 |
| x |
故选D
点评：在选择题中考查函数的基本性质，常用到数形结合的思想，所以必须熟练准确地掌握基本初函数的图象及性质，以及常见的图象变换方法．
练习册系列答案
相关题目
已知集合A={x|y=2x}，B={y|y=2x}，则A∩B=（ ）
| A、[0，+∞） | B、（0，+∞） | C、R | D、∅ |
设集合A={x||x-1|≤2}，B={x|x2-3x-4≤0}，则∁R（A∩B）=（ ）
| A、（-∞，-1）∪（1，+∞） | B、（-∞，3）∪（4，+∞） | C、（-∞，2）∪（2，+∞） | D、（-∞，-1）∪（3，+∞） |
下列四个图中，哪个可能是函数y=
的图象（ ）
| 10ln|x+1| |
| x+1 |
A、 |
B、 |
C、 |
D、 |
如图，半径为1的圆O与等边三角形ABC夹在两平行直线l1，l2之间，l∥l1与圆相交于F，G两点．与三角形ABC两边交于E，D两点，设弧
如果函数f（x）在[a，b]上的最大值和最小值分别为M、m，那么m（b-a）≤△
f（x）≤M（b-a）．根据这一结论求出△
2 -x2的取值范围（ ）
b a |
2 -1 |
| A、[0，3] | ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知函数f（x）=-2x3-x，若x1，x2，x3∈R，且x1+x2＞0，x2+x3＞0，x3+x1＞0，则f（x1）+f（x2）+f（x3）的值（ ）
| A、大于零 | B、小于零 | C、等于零 | D、大于零或小于零 |
定义区间[x1，x2]的长度为x2-x1．若函数y=|log2x|的定义域为[a，b]，值域为[0，2]，则区间[a，b]的长度的最大值为（ ）
A、
| ||
B、
| ||
| C、3 | ||
D、
|
已知函数f（x）=
，则f（1+log23）的值为（ ）
|
| A、6 | B、12 | C、24 | D、36 |