题目内容
(14分)(2011•广东)设a>0,讨论函数f(x)=lnx+a(1﹣a)x2﹣2(1﹣a)x的单调性.
见解析
试题分析:求出函数的定义域,求出导函数,设g(x)=2a(1﹣a)x2﹣2(1﹣a)x+1,x∈(0,+∞),讨论a=1,a>1与0<a<1三种情形,然后利用函数的单调性与导函数符号的关系求出单调性.
解:定义域{x|x>0}
f′(x)=
 =
=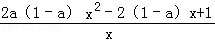
设g(x)=2a(1﹣a)x2﹣2(1﹣a)x+1,x∈(0,+∞)
①若a=1,则g(x)=1>0
∴在(0,+∞)上有f'(x)>0,即f(x)在(0,+∞)上是增函数.
②若a>1则2a(1﹣a)<0,g(x)的图象开口向下,
此时△=[﹣2(1﹣a)]2﹣4×2a(1﹣a)×1=4(1﹣a)(1﹣3a)>0
方程2a(1﹣a)x2﹣2(1﹣a)x+1=0有两个不等的实根
不等的实根为x1=
 ,x2=
,x2=
且x1<0<x2
∴在(0,
 )上g(x)>0,
)上g(x)>0,即f'(x)>0,f(x)是增函数;
在(
 ,+∞)上g(x)<0,
,+∞)上g(x)<0,即f'(x)<0,f(x)是减函数;
③若0<a<1则2a(1﹣a)>0,g(x)的图象开口向上,
此时△=[﹣2(1﹣a)]2﹣4×2a(1﹣a)×1=4(1﹣a)(1﹣3a)
可知当
 ≤a<1时,△≤0,故在(0,+∞)上,g(x)≥0,
≤a<1时,△≤0,故在(0,+∞)上,g(x)≥0,即f'(x)≥0,f(x)是增函数;
当0<a<
 时,△>0,方程2a(1﹣a)x2﹣2(1﹣a)x+1=0有两个不等的实根
时,△>0,方程2a(1﹣a)x2﹣2(1﹣a)x+1=0有两个不等的实根不等的实根满足
 >
> >0
>0故在(0,
 )和(
)和( ,+∞)上g(x)>0,
,+∞)上g(x)>0,即f'(x)>0,f(x)是增函数;
在(
 ,
, )上g(x)<0,
)上g(x)<0,即f'(x)<0,f(x)是减函数.
点评:本题考查利用导函数讨论函数的单调性:导函数为正函数递增;导函数为负,函数递减,同时考查了分类讨论的数学思想方法,属于难题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 ,
, .
. 时,证明:
时,证明: ;
; ,求k的取值范围.
,求k的取值范围.
 的最大值;
的最大值;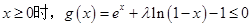 ,求
,求 的取值范围.
的取值范围. +
+
 (n
(n )
) ,
,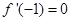 .
. 的单调区间;
的单调区间; ,都有
,都有 ,求
,求 的取值范围.
的取值范围. 是R上的单调函数,则实数m的取值范围是( )。
是R上的单调函数,则实数m的取值范围是( )。


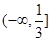

 ,
, ,
, ,其中
,其中 。
。 与
与 的图像在交点(2,
的图像在交点(2, )处的切线互相垂直,
)处的切线互相垂直, 的值;
的值; 是函数
是函数 的一个极值点,
的一个极值点, 和1是
和1是
 ,求
,求 ;
; 时,若
时,若 ,
, 是
是 -
- |
|
 ,函数
,函数 ,
, .
.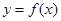 与曲线
与曲线 在它们的交点
在它们的交点 处的切线互相垂直,求
处的切线互相垂直,求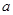 ,
, 的值;
的值; ,若对任意的
,若对任意的 ,且
,且 ,都有
,都有 ,求
,求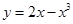 在横坐标为
在横坐标为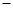 l的点处的切线为
l的点处的切线为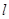 ,则直线
,则直线



 ,若
,若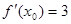 ,则
,则 ( )
( )


