题目内容
用0,1,2,3,4,5这六个数字
(Ⅰ)可组成多少个无重复数字的五位数?
(Ⅱ)可组成多少个无重复数字的五位奇数?
(Ⅲ)可组成多少个无重复数字的能被5整除的五位数?
(Ⅰ)可组成多少个无重复数字的五位数?
(Ⅱ)可组成多少个无重复数字的五位奇数?
(Ⅲ)可组成多少个无重复数字的能被5整除的五位数?
(I)分两类,第一类、个位为0的有
个;
第二类,个位不为0的有
×
×
个;
∴
+
×
×
=600个,
(II)依据个位为奇数的数是奇数,∴个位是1,3,5;
分三步:第一步,排个位有
种方法;
第二步,排万位有
种方法;
第三步,排余下的十位、百位、千位有
种方法;
由乘法原理得可组成
×
×
=288个无重复数字的五位奇数,
(III)依据能被5整除的数,其个位是0或5,
分两类,第一类,个位是0的有
个;
第二类,个位是5的,分两步,有
×
个;
由加法原理得可组成
+
×
=216个无重复数字的能被5整除的五位数.
| A | 45 |
第二类,个位不为0的有
| C | 15 |
| C | 14 |
| A | 34 |
∴
| A | 45 |
| C | 15 |
| C | 14 |
| A | 34 |
(II)依据个位为奇数的数是奇数,∴个位是1,3,5;
分三步:第一步,排个位有
| C | 13 |
第二步,排万位有
| C | 14 |
第三步,排余下的十位、百位、千位有
| A | 34 |
由乘法原理得可组成
| C | 13 |
| C | 14 |
| A | 34 |
(III)依据能被5整除的数,其个位是0或5,
分两类,第一类,个位是0的有
| A | 45 |
第二类,个位是5的,分两步,有
| C | 14 |
| A | 34 |
由加法原理得可组成
| A | 45 |
| C | 14 |
| A | 34 |

练习册系列答案
相关题目

 的展开式中的常数项是 .
的展开式中的常数项是 .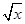 -
-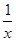 )6的展开式中所有有理项的系数和等于________.(用数字作答)
)6的展开式中所有有理项的系数和等于________.(用数字作答)