题目内容
已知P(x,y),A(-1,0),向量 与
与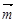 =(1,1)共线。
=(1,1)共线。
(1)求y关于x的函数解析式;
(2)是否在直线y=2x和直线y=3x上分别存在一点B、C,使得满足∠BPC为锐角时x取值集合为{x| x<-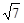 或x>
或x>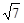 }?若存在,求出这样的B、C的坐标;若不存在,说明理由。
}?若存在,求出这样的B、C的坐标;若不存在,说明理由。
(1)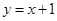 (2)存在 B(2,4),C(-1,-3)或
(2)存在 B(2,4),C(-1,-3)或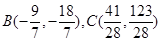
解析试题分析:(1)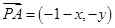 与
与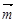 =(1,1)共线,所以
=(1,1)共线,所以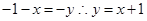
(2)存在 B(2,4),C(-1,-3)或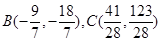
设B(b,2b),C(c,3c),∠BPC为锐角 等价于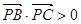
得
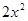 +(2-3b-4c)x+1-2b-3c+7bc>0,因为解集是{x| x<-
+(2-3b-4c)x+1-2b-3c+7bc>0,因为解集是{x| x<-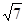 或x>
或x>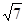 }
}
(2-3b-4c)=0,1-2b-3c+7bc=-14
解得b=" 2" ,c=" -1" 或b=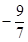 ,c=
,c=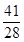
考点:向量运算及向量共线
点评:两向量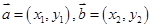 共线,则有
共线,则有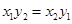 ,第二问中将角看做两向量夹角,从而将确定角的范围转化为向量数量积满足的条件
,第二问中将角看做两向量夹角,从而将确定角的范围转化为向量数量积满足的条件

练习册系列答案
相关题目
平面向量 ,
, ,
,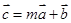 (
( ),且
),且 与
与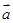 的夹角等于
的夹角等于 与
与 的夹角,则
的夹角,则 ( )
( )
A.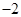 | B. | C. | D. |
 ,点
,点 为直线
为直线 上的一个动点.
上的一个动点. 恒为锐角;
恒为锐角; 为菱形,求
为菱形,求 的值.
的值.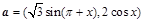 ,
,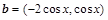 ,已知函数
,已知函数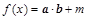 在
在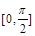 上的最大值为6.
上的最大值为6. 的值;
的值;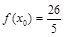 ,
,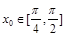 .求
.求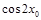 的值.
的值.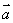 =(
=(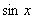 ,1),
,1),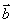 =(
=(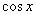 ,1),
,1),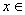 R.
R.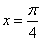 时,求向量
时,求向量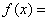 |
|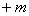 为奇函数,求实数
为奇函数,求实数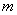 的值.
的值.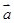 =(1,2),
=(1,2),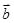 =(2,-2).
=(2,-2).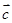 =4
=4
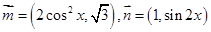 ,函数
,函数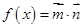
 的单调增区间;
的单调增区间;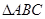 中,
中,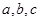 分别是角A, B, C的对边,且
分别是角A, B, C的对边,且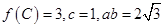 ,且
,且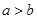
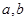 的值.
的值.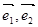 是两个不共线的向量,
是两个不共线的向量,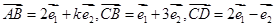 ,若A、B、D三点共线,求k的值.。
,若A、B、D三点共线,求k的值.。 =a,
=a, =b,试用a、b表示
=b,试用a、b表示 和
和 ,则
,则