题目内容
如图，已知定点A(2 ，1) ，F(1 ，0) 是椭圆
的一个焦点，P是椭圆上的点，求：|PA|+|PF|的最值，
的一个焦点，P是椭圆上的点，求：|PA|+|PF|的最值，
解：∵焦点F(1 ，0) 在x 轴上,
∴m2-8=1 ，即m=9 ，
∴椭圆方程为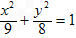
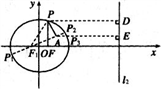
如图，设左焦点为F1，
|PA|+|PF|=|PA|+2a-|PF1| =6+(|PA|-|PF1|).连结AF1并延长交椭圆于点P1，反向延长AF1交椭圆于点P2，P1、P2分别使|PA|+|PF|取得最大值和最小值，
即|PA|+|PF|的最大值为6+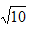
，最小值为6-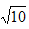
∴m2-8=1 ，即m=9 ，
∴椭圆方程为
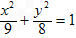
如图，设左焦点为F1，
|PA|+|PF|=|PA|+2a-|PF1| =6+(|PA|-|PF1|).连结AF1并延长交椭圆于点P1，反向延长AF1交椭圆于点P2，P1、P2分别使|PA|+|PF|取得最大值和最小值，
即|PA|+|PF|的最大值为6+
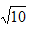，最小值为6-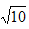
练习册系列答案
名校课堂系列答案
相关题目
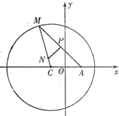如图，已知定点A（1，0），定圆C：（x+1）2+y2=8，M为圆C上的一个动点，点P在线段AM上，点N在线段CM上，且满足
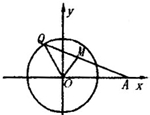如图，已知定点A（2，0），点Q是圆x2+y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程．
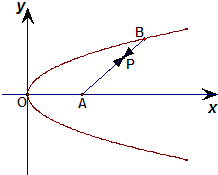如图，已知定点A（2，0）及抛物线y2=x，点B在该抛物线上，若动点P使得