题目内容
如图，已知定点A(2，0)，点Q是圆x2＋y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程.
解:由三角形的内角平分线性质，得
＝
＝
，∴
＝
.
设M、Q的坐标分别为(x，y)、(x0，y0)，则
∴
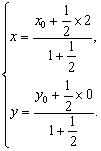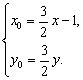
∵Q在圆x2＋y2=1上，∴x02＋y02＝1.
∴(
x－1)2＋(
y)2＝1.
∴动点M的轨迹方程为(x－
)2＋y2＝
.
点评:注意三角形内角平分线性质的应用.解析几何结合平面图形的性质，有时能起到事半功倍的效果.
练习册系列答案
相关题目
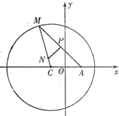如图，已知定点A（1，0），定圆C：（x+1）2+y2=8，M为圆C上的一个动点，点P在线段AM上，点N在线段CM上，且满足
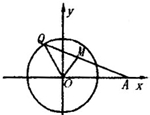如图，已知定点A（2，0），点Q是圆x2+y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程．
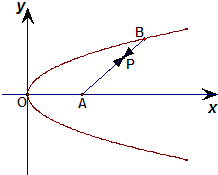如图，已知定点A（2，0）及抛物线y2=x，点B在该抛物线上，若动点P使得
的一个焦点，P是椭圆上的点，求：|PA|+|PF|的最值，