题目内容
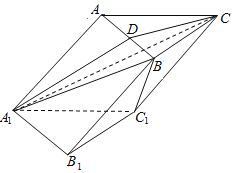
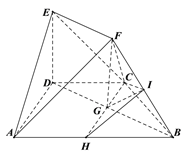
【题目】如图,在四边形ABCD中,AB//CD,∠ABD=30°,AB=2CD=2AD=2,DE⊥平面ABCD,EF//BD,且BD=2EF.
(Ⅰ)求证:平面ADE⊥平面BDEF;
(Ⅱ)若二面角C![]() BF
BF![]() D的大小为60°,求CF与平面ABCD所成角的正弦值.
D的大小为60°,求CF与平面ABCD所成角的正弦值.

【答案】(1)见解析(2)![]()
【解析】分析:(1)根据面面垂直的判定定理即可证明平面ADE⊥平面BDEF;
(2)建立空间直角坐标系,利用空间向量法即可求CF与平面ABCD所成角的正弦值;也可以应用常规法,作出线面角,放在三角形当中来求解.
详解:(Ⅰ)在△ABD中,∠ABD=30°,由AO2=AB2+BD2-2AB·BDcos30°,
解得BD=![]() ,所以AB2+BD2=AB2,根据勾股定理得∠ADB=90°∴AD⊥BD.
,所以AB2+BD2=AB2,根据勾股定理得∠ADB=90°∴AD⊥BD.
又因为DE⊥平面ABCD,AD![]() 平面ABCD,∴AD⊥DE.
平面ABCD,∴AD⊥DE.
又因为BD![]() DE=D,所以AD⊥平面BDEF,又AD
DE=D,所以AD⊥平面BDEF,又AD![]() 平面ABCD,
平面ABCD,
∴平面ADE⊥平面BDEF,
(Ⅱ)方法一:
如图,由已知可得![]() ,
,![]() ,则
,则
![]() ,则三角形BCD为锐角为30°的等腰三角形.
,则三角形BCD为锐角为30°的等腰三角形.
![]() 则
则![]() .
.
过点C做![]() ,交DB、AB于点G,H,则点G为点F在面ABCD上的投影.连接FG,则
,交DB、AB于点G,H,则点G为点F在面ABCD上的投影.连接FG,则
![]() ,DE⊥平面ABCD,则
,DE⊥平面ABCD,则![]() 平面
平面![]() .
.
过G做![]() 于点I,则BF
于点I,则BF![]() 平面
平面![]() ,即角
,即角![]() 为
为
二面角C![]() BF
BF![]() D的平面角,则
D的平面角,则![]() 60°.
60°.
则![]() ,
,![]() ,则
,则![]() .
.
在直角梯形BDEF中,G为BD中点,![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,则
,则![]() .
.
![]() ,则
,则![]() ,即CF与平面ABCD所成角的正弦值为
,即CF与平面ABCD所成角的正弦值为![]() .
.
(Ⅱ)方法二:
 可知DA、DB、DE两两垂直,以D为原点,建立如图所示的空间直角坐标系D-xyz.
可知DA、DB、DE两两垂直,以D为原点,建立如图所示的空间直角坐标系D-xyz.
设DE=h,则D(0,0,0),B(0,![]() ,0),C(-
,0),C(-![]() ,-
,-![]() ,h).
,h).
![]() ,
,![]() .
.
设平面BCF的法向量为m=(x,y,z),
则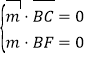 所以
所以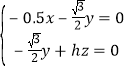 取x=
取x=![]() ,所以m=(
,所以m=(![]() ,-1
,-1![]() ),
),
取平面BDEF的法向量为n=(1,0,0),
由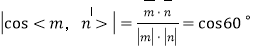 ,解得
,解得![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() ,设CF与平面ABCD所成角为
,设CF与平面ABCD所成角为![]() ,
,
则sin![]() =
=![]() .
.
故直线CF与平面ABCD所成角的正弦值为![]()

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】利用独立性检验的方法调查高中生的写作水平与离好阅读是否有关,随机询问120名高中生是否喜好阅读,利用2×2列联表,由计算可得K2=4.236
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表,可得正确的结论是( )
A.有95%的把握认为“写作水平与喜好阅读有关”
B.有97.5%的把握认为“写作水平与喜好阅读有关”
C.有95%的把握认为“写作水平与喜好阅读无关”
D.有97.5%的把握认为“写作水平与喜好阅读无关”