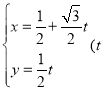Question

【题目】已知函数f(x)＝2|x＋1|＋|x－2|.

(1)求f(x)的最小值m；

(2)若a，b，c均为正实数，且满足a＋b＋c＝m，求证：＋＋≥3.

Answer 1

【答案】（1）m＝3 （2）证明见解析

【解析】

（1）分段讨论当x＜－1时，当－1≤x＜2时，当x≥2时，函数f(x)的值域，然后求函数在定义域上的值域即可；

（2）由已知条件a＋b＋c＝3，再结合重要不等式证明即可.

解：（1）当x＜－1时，f(x)＝－2(x＋1)－(x－2)＝－3x∈(3，＋∞)；

当－1≤x＜2时，f(x)＝2(x＋1)－(x－2)＝x＋4∈[3,6)；

当x≥2时，f(x)＝2(x＋1)＋(x－2)＝3x∈[6，＋∞)．

即，

综上，f(x)的最小值m＝3.

（2）证明：因为a，b，c均为正实数，且满足a＋b＋c＝3，

所以＋＋＋(a＋b＋c)

＝＋＋

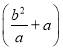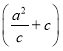
≥2

＝2(a＋b＋c)，

当且仅当a＝b＝c＝1时，取“＝”，

所以＋＋≥a＋b＋c，

又a＋b＋c＝3，

即＋＋≥3.