题目内容
【题目】已知x=1是函数f(x)=![]() ax3-
ax3-![]() x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.
(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
【答案】(1)f(x)的解析式为f(x)=![]() x3-
x3-![]() x2+2x+5; (2)m的取值范围为
x2+2x+5; (2)m的取值范围为![]()
【解析】试题分析:(I)利用三次函数在极值点处的导数为零,即可解得a的值,进而确定函数的解析式;(II)将两曲线有三个交点问题,转化为函数g(x)=f(x)﹣(2x+m)有三个零点问题,利用导数研究函数g(x)的单调性和极值,找到问题的充要条件,列不等式即可解得m的范围
试题解析:
解:(1)依题意f′(x)=ax2-3x+a+1,
由f′(1)=0得a=1,
∴函数f(x)的解析式为f(x)=![]() x3-
x3-![]() x2+2x+5.
x2+2x+5.
(2)曲线y=f(x)与直线y=2x+m有三个交点,
即![]() x3-
x3-![]() x2+2x+5-2x-m=0有三个实数根,
x2+2x+5-2x-m=0有三个实数根,
令g(x)=![]() x3-
x3-![]() x2+2x+5-2x-m=
x2+2x+5-2x-m=![]() x3-
x3-![]() x2+5-m,则g(x)有三个零点.
x2+5-m,则g(x)有三个零点.
由g′(x)=x2-3x=0得x=0或x=3.
令g′(x)>0得x<0或x>3;令g′(x)<0得0<x<3.
∴函数g(x)在(-∞,0)上为增函数,在(0,3)上为减函数,在(3,+∞)上为增函数.
∴函数在x=0处取得极大值,在x=3处取得极小值.
要使g(x)有三个零点,只需 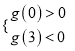 解得
解得![]() <m<5.
<m<5.
∴实数m的取值范围为![]() .
.

练习册系列答案
相关题目