题目内容
现有甲、乙两个靶,其射手向甲靶射击一次,命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
(1)求该射手恰好命中一次的概率;
(2)求该射手的总得分X的分布列.
| 3 |
| 4 |
| 2 |
| 3 |
(1)求该射手恰好命中一次的概率;
(2)求该射手的总得分X的分布列.
(1)若只命中甲靶,概率为
×(1-
)2=
,若只命中乙靶一次,概率为(1-
)•
•
•
=
,
故该射手恰好命中一次的概率为
+
=
.
(2)由题意可得该射手的总得分X的值可为:0,1,2,3,4,5,
P(X=0)=
×(
)2=
,P(X=1)=
×(
)2=
,P(X=2)=
•
•
•
=
,P(X=3)=
•
•
•
=
,
P(X=4)=
×(
)2=
,P(X=5)=
×(
)2=
.
故该射手的总得分X的分布列为:
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 12 |
| 3 |
| 4 |
| C | 12 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
故该射手恰好命中一次的概率为
| 1 |
| 12 |
| 1 |
| 9 |
| 7 |
| 36 |
(2)由题意可得该射手的总得分X的值可为:0,1,2,3,4,5,
P(X=0)=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 36 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 4 |
| C | 12 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 3 |
| 4 |
| C | 12 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
P(X=4)=
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 9 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
故该射手的总得分X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 的分布列.
的分布列. ,否则其获胜的概率为
,否则其获胜的概率为 .
. 为比赛结束时甲的得分,求随机变量
为比赛结束时甲的得分,求随机变量 .
.

 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 ;
; 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递减”为事件
在定义域内单调递减”为事件 ,求事件
,求事件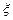 的分布列和数学期望.
的分布列和数学期望.