题目内容
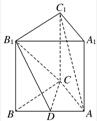 如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5,cos∠BAC=
如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5,cos∠BAC= .
.
(1)求证:BC⊥AC1;
(2)若D是AB的中点,求证:AC1∥平面CDB1.
证明:(1)∵在△ABC中,AC=3,AB=5,
cos∠BAC= ,
,
∴BC2=AB2+AC2-2AB•AC•
cos∠BAC=25+9-2×5×3× =16.
=16.
∴BC=4,∠ACB=90°,
∴BC⊥AC,
∵BC⊥CC1,AC∩CC1=C,
∴BC⊥平面ACC1A1,
∵AC1?平面ACC1A1,
∴BC⊥AC1.
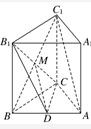
(2)连接BC1交B1C于M,则M为BC1的中点,
连接DM,则DM∥AC1,
∵DM?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
分析:(1)证明BC⊥AC,BC⊥CC1,AC、CC1是平面ACC1A1内的两条相交直线,即可证明BC⊥平面ACC1A1,从而证明BC⊥AC1;
(2)D是AB的中点,连接BC1交B1C于M,连接DM,证明DM∥AC1,即可证明AC1∥平面CDB1.
点评:本题考查直线与平面平行的判定,直线与直线的垂直,是基础题.
cos∠BAC=
 ,
,∴BC2=AB2+AC2-2AB•AC•
cos∠BAC=25+9-2×5×3×
 =16.
=16.∴BC=4,∠ACB=90°,
∴BC⊥AC,
∵BC⊥CC1,AC∩CC1=C,
∴BC⊥平面ACC1A1,
∵AC1?平面ACC1A1,
∴BC⊥AC1.

(2)连接BC1交B1C于M,则M为BC1的中点,
连接DM,则DM∥AC1,
∵DM?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
分析:(1)证明BC⊥AC,BC⊥CC1,AC、CC1是平面ACC1A1内的两条相交直线,即可证明BC⊥平面ACC1A1,从而证明BC⊥AC1;
(2)D是AB的中点,连接BC1交B1C于M,连接DM,证明DM∥AC1,即可证明AC1∥平面CDB1.
点评:本题考查直线与平面平行的判定,直线与直线的垂直,是基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目




