题目内容
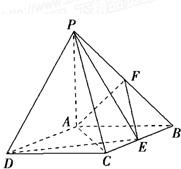 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=| 3 |
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有PE⊥AF;
(3)当BE为何值时,PA与平面PDE所成角的大小为45°?
分析:(1)当点E为BC的中点时,EF与平面PAC平行.由线面平行的判定定理可以证出结论.用线面平行的判定定理证明时要注意把条件写全.
(2) 无论点E在BC边的何处,都有PE⊥AF,可建立空间坐标系设点E(x,1,0),求出两向量PE、AF的坐标,用内积为0证两线垂直.
(3)求出用E的坐标表示的平面PDE的法向量,由线面角的向量表示公式建立方程求出E的坐标.
(2) 无论点E在BC边的何处,都有PE⊥AF,可建立空间坐标系设点E(x,1,0),求出两向量PE、AF的坐标,用内积为0证两线垂直.
(3)求出用E的坐标表示的平面PDE的法向量,由线面角的向量表示公式建立方程求出E的坐标.
解答: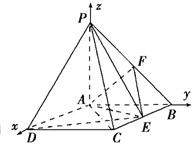 解:(1)当点E为BC的中点时,EF与平面PAC平行.
解:(1)当点E为BC的中点时,EF与平面PAC平行.
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC.
又EF?平面PAC,而PC?平面PAC,
∴EF∥平面PAC.
(2)证明:建立如图所示空间直角坐标系,则
P(0,0,1),B(0,1,0),
F(0,
,
),D(
,0,0),
设BE=x(0≤x≤
),
则E(x,1,0),
;
•
=(x,1,-1)•(0,
,
)=0,
∴PE⊥AF.
(3)设平面PDE的法向量为m=(p,q,1),
由
,得m=(
,1-
,1).
而
=(0,0,1),依题意PA与平面PDE所成角为45°,
所以sin45°=
,
∴
=
,
得BE=x=
-
或BE=x=
+
>
(舍).
故BE=
-
时,PA与平面PDE所成角为45°.
 解:(1)当点E为BC的中点时,EF与平面PAC平行.
解:(1)当点E为BC的中点时,EF与平面PAC平行.∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC.
又EF?平面PAC,而PC?平面PAC,
∴EF∥平面PAC.
(2)证明:建立如图所示空间直角坐标系,则
P(0,0,1),B(0,1,0),
F(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
设BE=x(0≤x≤
| 3 |
则E(x,1,0),
;
| PE |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
∴PE⊥AF.
(3)设平面PDE的法向量为m=(p,q,1),
由
|
| 1 | ||
|
| x | ||
|
而
| AP |
所以sin45°=
| ||
| 2 |
∴
| 1 | ||||||||
|
| 1 | ||
|
得BE=x=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故BE=
| 3 |
| 2 |
点评:考查用向量证明立体几何中的问题,此类题的做题步骤一般是先建立坐标系,设出坐标,用线的方向向量的内积为0证线线垂直,线面垂直,用线的方向向量与面的法向量的垂直证面面平行,两者的共线证明线面垂直.此处为一规律性较强的题,要注意梳理清楚思路.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=