题目内容
(2013•闵行区二模)给出下列四个命题:
①如果复数z满足|z+i|+|z-i|=2,则复数z在复平面的对应点的轨迹是椭圆.
②若对任意的n∈N*,(an+1-an-1)(an+1-2an)=0恒成立,则数列{an}是等差数列或等比数列.
③设f(x)是定义在R上的函数,且对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)是R上的奇函数或偶函数.
④已知曲线C:
-
=1和两定点E(-5,0)、F(5,0),若P(x,y)是C上的动点,则||PE|-|PF||<6.
上述命题中错误的个数是( )
①如果复数z满足|z+i|+|z-i|=2,则复数z在复平面的对应点的轨迹是椭圆.
②若对任意的n∈N*,(an+1-an-1)(an+1-2an)=0恒成立,则数列{an}是等差数列或等比数列.
③设f(x)是定义在R上的函数,且对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)是R上的奇函数或偶函数.
④已知曲线C:
|
|
上述命题中错误的个数是( )
分析:①依据|Z+i|+|Z-i|=2的几何意义得到对应点的轨迹是线段;
②由于对任意的n∈N*,(an+1-an-1)(an+1-2an)=0恒成立,
则由两因式分别为0,可求出数列{an}的递推公式,继而可得到数列是等差数列或等比数列;
③由于对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)=f(-x)或f(x)=-f(-x),则可判断函数的奇偶性;
④若设P(x,y)(x>0,y≥0),则可将曲线C:
-
=1化简为
-
=1(x>0,y≥0)
再画出图形,找到特殊点,当y=0时,即可求出||PE|-|PF||的值,继而判断正误.
②由于对任意的n∈N*,(an+1-an-1)(an+1-2an)=0恒成立,
则由两因式分别为0,可求出数列{an}的递推公式,继而可得到数列是等差数列或等比数列;
③由于对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)=f(-x)或f(x)=-f(-x),则可判断函数的奇偶性;
④若设P(x,y)(x>0,y≥0),则可将曲线C:
|
|
| x |
| 3 |
| y |
| 4 |
再画出图形,找到特殊点,当y=0时,即可求出||PE|-|PF||的值,继而判断正误.
解答:解:①|Z+i|表示复平面上,点Z与点-i的距离,|Z-i|表示复平面上,点Z与点i的距离,
∴|Z+i|+|Z-i|=2,表示复平面上,点Z与点i、-i的距离之和等于2.则对应点的轨迹是线段,故①错;
②由于对任意的n∈N*,(an+1-an-1)(an+1-2an)=0恒成立,
则(an+1-an-1)=0或(an+1-2an)=0,所以an+1-an=1或an+1=2an,则数列{an}是等差数列或等比数列,故②正确;
③由于对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)=f(-x)或f(x)=-f(-x),则f(x)是R上的偶函数或奇函数,故③正确;
④设P(x,y)(x>0,y≥0)是C上的动点曲线C:
-
=1,则
-
=1(x>0,y≥0)
又由于两定点E(-5,0)、F(5,0),则P、E、F三点位置如图示.
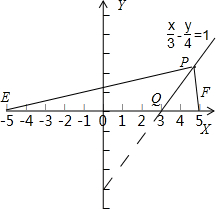
当y=0时,P点与Q点重合,即||PE|-|PF||=||QE|-|QF||=6,故④错误.
故答案为 B.
∴|Z+i|+|Z-i|=2,表示复平面上,点Z与点i、-i的距离之和等于2.则对应点的轨迹是线段,故①错;
②由于对任意的n∈N*,(an+1-an-1)(an+1-2an)=0恒成立,
则(an+1-an-1)=0或(an+1-2an)=0,所以an+1-an=1或an+1=2an,则数列{an}是等差数列或等比数列,故②正确;
③由于对任意的x∈R,|f(x)|=|f(-x)|恒成立,则f(x)=f(-x)或f(x)=-f(-x),则f(x)是R上的偶函数或奇函数,故③正确;
④设P(x,y)(x>0,y≥0)是C上的动点曲线C:
|
|
| x |
| 3 |
| y |
| 4 |
又由于两定点E(-5,0)、F(5,0),则P、E、F三点位置如图示.
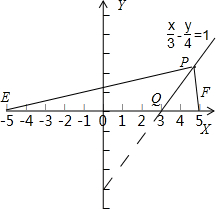
当y=0时,P点与Q点重合,即||PE|-|PF||=||QE|-|QF||=6,故④错误.
故答案为 B.
点评:本题考查的知识点是,判断命题真假,属于基础题.我们需对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目