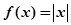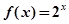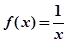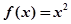题目内容
(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
(1)从第4年开始获取纯利润。
(2)两种方案获利一样多,而方案(1)时间比较短,所以选择方案(1)。
(2)两种方案获利一样多,而方案(1)时间比较短,所以选择方案(1)。
试题分析:(1)设第n年获取利润为y万元,n年共收入租金30n万元.付出装修费共
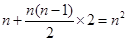 ,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.
,付出投资81万元,由此可知利润y=30n-(81+n2),由y>0能求出从第几年开始获取纯利润.(2)①纯利润总和最大时,以10万元出售,利用二次函数的性质求出最大利润,方案②利用基本不等式进行求解,当两种方案获利一样多,就看时间哪个方案短就选择哪个..
(1)设第
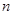 年获取利润为
年获取利润为 万元。………………1分
万元。………………1分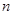 年共收租金30
年共收租金30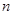 万元,付出装修费构成一个以1为首项,2为公差的等差数列,
万元,付出装修费构成一个以1为首项,2为公差的等差数列,共
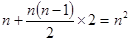 …………………2分
…………………2分因此利润
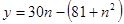 令
令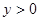 ……………4分
……………4分解得
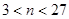 ……………5分
……………5分所以从第4年开始获取纯利润。………………6分
(2)年平均利润
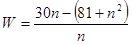 ………………8分
………………8分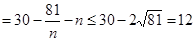 ………………9分
………………9分(当且仅当
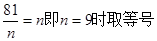 )所以9年后共获利润:154万元。……………10分
)所以9年后共获利润:154万元。……………10分利润
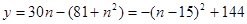
所以15年后共获利润:144+10=154万元……………………11分
两种方案获利一样多,而方案(1)时间比较短,所以选择方案(1)。…………………12分
点评:本题是函数模型选取问题,在直接比较不能凑效的前提下可考虑作差法比较.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

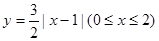



 ,(1)求
,(1)求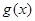 的解析式;(2)求
的解析式;(2)求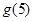 的值。
的值。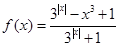
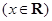 的最大值为
的最大值为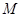 ,最小值为
,最小值为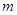 ,
,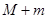 的值为 .
的值为 .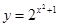 的值域是 .
的值域是 .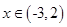 ,求函数
,求函数 =
=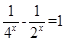 的最大值与最小值.
的最大值与最小值.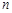 ,定义“
,定义“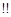 ”如下:当
”如下:当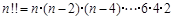 ,
, 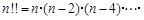
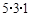 .现在有如下四个命题:
.现在有如下四个命题: 的个位数是0;
的个位数是0; 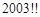 的个位数是5;
的个位数是5;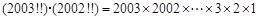 ;
; 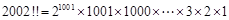 ;
;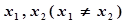 ,
,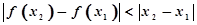 恒成立”的函数叫Ω函数,则下面四个函数中,属于Ω函数的是( )
恒成立”的函数叫Ω函数,则下面四个函数中,属于Ω函数的是( )