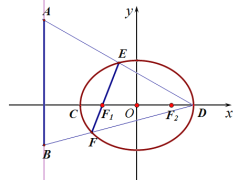
题目内容
【题目】已知抛物线![]() (
(![]() )经过点
)经过点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() .
.
(1)若直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若直线![]() 过点
过点![]() ,设
,设![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() 且
且![]() 且
且![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意易得直线斜率存在且不为![]() ,且直线
,且直线![]() 、
、![]() 斜率存在,设出直线方程,并联立抛物线方程,根据交点有两个,得出
斜率存在,设出直线方程,并联立抛物线方程,根据交点有两个,得出![]() ,解不等式即可得直线斜率的范围.
,解不等式即可得直线斜率的范围.
(2)根据![]() ,
,![]() ,得出
,得出![]() 、
、![]() 与点
与点![]() 坐标之间的关系,再根据
坐标之间的关系,再根据![]() 在同一直线上,
在同一直线上,![]() 在同一直线上,得出
在同一直线上,得出![]() ,
,![]() 与点
与点![]() 坐标之间的关系,根据(1)中联立所得的方程得出点
坐标之间的关系,根据(1)中联立所得的方程得出点![]() 横坐标之间的关系,对原式进行化简,即可得
横坐标之间的关系,对原式进行化简,即可得![]() 的值.
的值.
(3) 设直线![]() 的方程为:
的方程为:![]() 联立直线与抛物线的方程得出点
联立直线与抛物线的方程得出点![]() 纵坐标之间的关系,再由
纵坐标之间的关系,再由![]() ,
,![]() ,得出
,得出![]() 、
、![]() 与点
与点![]() 坐标之间的关系,对
坐标之间的关系,对![]() 化简可求得
化简可求得![]() 的值.
的值.
(1)因为抛物线![]() 经过点
经过点![]() ,所以
,所以![]() ,所以
,所以![]() ,所以抛物线
,所以抛物线![]() 的解析式为
的解析式为![]() 。
。
又因为直线![]() 过点
过点![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 有两个不同的交点,易知直线
有两个不同的交点,易知直线![]() 斜率存在且不为
斜率存在且不为![]() ,故可设直线
,故可设直线![]() 的方程式为
的方程式为![]() .
.
根据题意可知直线![]() 不能过点
不能过点![]() ,所以直线
,所以直线![]() 的斜率
的斜率![]() .
.
若直线![]() 与抛物线的一个交点为
与抛物线的一个交点为![]() ,此时该点与点
,此时该点与点![]() 所在的直线斜率不存在,则该直线与
所在的直线斜率不存在,则该直线与![]() 轴无交点,与题目条件矛盾,
轴无交点,与题目条件矛盾,
此时![]() ,所以直线
,所以直线![]() 斜率
斜率![]() .
.
联立方程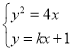 ,得
,得![]() ,
,
因为直线![]() 与抛物线有两个不同的交点,所以
与抛物线有两个不同的交点,所以![]() ,所以
,所以![]() 。
。
故直线![]() 的斜率
的斜率![]() 的取值范围是
的取值范围是![]() 且
且![]() 且
且![]() .
.
(2)设点![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,故
,故![]() ,由
,由![]() 得
得![]() ,
,
设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为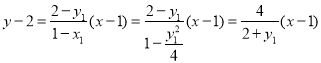 ,
,
令![]() ,得
,得![]() ①,由直线
①,由直线![]() 可得
可得![]() ②,
②,
因为![]() ③,将①②代入③可得,
③,将①②代入③可得,
![]()
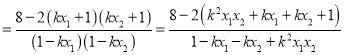 ,
,
又由根与系数的关系:![]() ,
,![]() ,
,
所以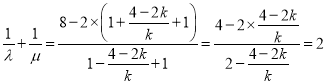 ,
,
所以![]() .
.
(3)设直线![]() 的方程为:
的方程为:![]() 由
由![]() ,得
,得![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,∵
,∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴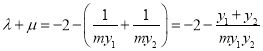
![]() ,
,
![]() .
.

 智慧小复习系列答案
智慧小复习系列答案【题目】菜市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况,首先随机抽样其中200名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图1所示的频率分布南方匿,接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价
)进行了一次调查统计,制成了如图1所示的频率分布南方匿,接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1﹣13分别对应2018年1月至2019年1月).
(单位:万元/平方米),制成了如图2所示的散点图(图中月份代码1﹣13分别对应2018年1月至2019年1月).
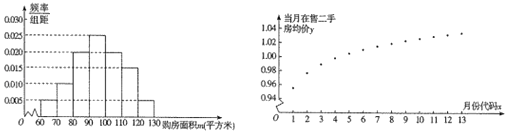
(1)试估计该市市民的平均购房面积![]() .
.
(2)现采用分层抽样的方法从购房耐积位于![]() 的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在
的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在![]() 的概率.
的概率.
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如表所示:
,并得到一些统计量的值,如表所示:
|
| |
|
|
|
|
| |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .参考公式:相关指数
.参考公式:相关指数 .
.