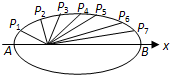
题目内容
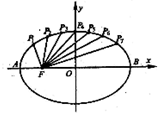 如图,把椭圆
如图,把椭圆| x2 |
| 25 |
| y2 |
| 16 |
35
35
.分析:利用椭圆的定义可求得|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=
×2a,结合椭圆的标准方程即可求得答案.
| 7 |
| 2 |
解答:解:∵椭圆的方程为
+
=1,
∴a=5,b=4,c=3.
∵F是椭圆的一个焦点,设F′为椭圆的另一焦点,
依题意|P1F|=|P7F′|,|P2F|=|P6F′|,|P3F|=|P4F′|,
∴|P1F|+|P7F|=|P2F|+|P6F|=|P3F|+|P4F|=2a=10,
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=
×2a=7a=35.
故答案为:35.
| x2 |
| 25 |
| y2 |
| 16 |
∴a=5,b=4,c=3.
∵F是椭圆的一个焦点,设F′为椭圆的另一焦点,
依题意|P1F|=|P7F′|,|P2F|=|P6F′|,|P3F|=|P4F′|,
∴|P1F|+|P7F|=|P2F|+|P6F|=|P3F|+|P4F|=2a=10,
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=
| 7 |
| 2 |
故答案为:35.
点评:本题考查椭圆的简单性质,着重考查椭圆的定义的应用,考查观察与分析、运算的能力,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
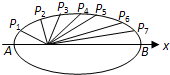 如图,把椭圆
如图,把椭圆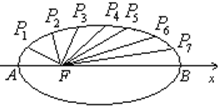 如图,把椭圆
如图,把椭圆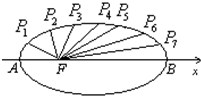 如图,把椭圆
如图,把椭圆