题目内容
【题目】已知函数![]() ,
, ![]()
![]() .
.
(I)当a=2时,求曲线y = ![]() 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(II)求函数![]() 在区间[0 , e -1]上的最小值.
在区间[0 , e -1]上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据点斜式求切线方程(2)先求导数,再根据定义区间分类讨论导函数符号变化规律:当
,再根据点斜式求切线方程(2)先求导数,再根据定义区间分类讨论导函数符号变化规律:当![]() 时,导数非负,函数为增函数;当
时,导数非负,函数为增函数;当![]() 时,导数非正,函数为减函数;当
时,导数非正,函数为减函数;当![]() 时,导数先负后正,函数先增后减,最后根据单调性确定最小值
时,导数先负后正,函数先增后减,最后根据单调性确定最小值
试题解析:(I)f (x)的定义域为![]() .
.
因为![]() ,a = 2,
,a = 2,
所以![]() ,
, ![]() .
.
所以 函数f (x)在点![]() 处的切线方程是
处的切线方程是 ![]() .
.
(II)由题意可得 ![]() .
.
(1)当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上为减函数,
上为减函数,
所以在区间![]() 上,
上, ![]() .
.
(2) 当![]() 时, 令
时, 令![]() ,则
,则![]() ,
,
① 当![]() ,即
,即![]() 时,
时,
对于![]() ,
, ![]() ,
,
所以f (x)在![]() 上为增函数,
上为增函数,
所以![]() .
.
② 当![]() ,即
,即![]() 时,
时,
对于![]() ,
, ![]() ,
,
所以f (x)在![]() 上为减函数,
上为减函数,
所以![]() .
.
③ 当![]() 即
即![]() 时,
时,
当x变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
| 0 |
|
|
|
|
| - | 0 | + | ||
|
| 极小值 |
|
所以 ![]() .
.
综上,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成3元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到频数表如下:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
将上表中的频率视为概率,回答下列问题:
(1)现从甲公司随机抽取3名送餐员,求恰有2名送餐员送餐单数超过40的概率;
(2)(i)记乙公司送餐员日工资为X(单位:元),求X的数学期望;
(ii)某人拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日平均工资的角度考虑,他应该选择去哪家公司应聘,说明理由.
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某大学社团为调查大学生对于“中华诗词”的喜好,在该校随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:
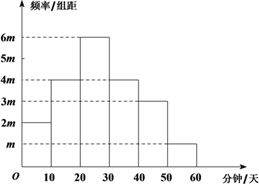
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
学习时间 (分钟/天) |
|
|
|
等级 | 一般 | 爱好 | 痴迷 |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 从该大学的学生中随机选出一人,试估计其“爱好”中华诗词的概率;
(Ⅲ) 假设同组中的每个数据用该组区间的右端点值代替,试估计样本中40名学生每人每天学习“中华诗词”的时间.