题目内容
(2013•临沂二模)在区间[-1,1]上任取两数m和n,则关于x的方程x2+mx+n2=0有两不相等实根的概率为
.
| 1 |
| 4 |
| 1 |
| 4 |
分析:本题是一个等可能事件的概率,试验发生包含的事件是在区间[-1,1]上任取两个数m和n,写出事件对应的集合,做出面积,满足条件的事件是关于x的方程x2+mx+n2=0有两不相等实根,根据二次方程的判别式写出m,n要满足的条件,写出对应的集合,做出面积,得到概率.
解答: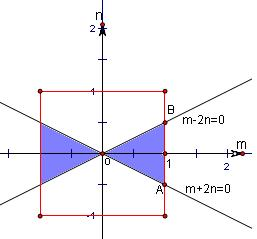 解:由题意知本题是一个等可能事件的概率,
解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[-1,1]上任取两个数m和n,
事件对应的集合是Ω={(m,n)|-1≤m≤1,-1≤n≤1}
对应的面积是sΩ=4,
满足条件的事件是关于x的方程x2+mx+n2=0有两不相等实根,
即m2-4n2≥0,
事件对应的集合是A={(m,n)|-1≤m≤1,-1≤n≤1,m2-4n2≥0}
对应的图形的面积是sA=1,即如图阴影部分的面积.
∴根据等可能事件的概率得到P=
.
故答案为:
.
 解:由题意知本题是一个等可能事件的概率,
解:由题意知本题是一个等可能事件的概率,∵试验发生包含的事件是在区间[-1,1]上任取两个数m和n,
事件对应的集合是Ω={(m,n)|-1≤m≤1,-1≤n≤1}
对应的面积是sΩ=4,
满足条件的事件是关于x的方程x2+mx+n2=0有两不相等实根,
即m2-4n2≥0,
事件对应的集合是A={(m,n)|-1≤m≤1,-1≤n≤1,m2-4n2≥0}
对应的图形的面积是sA=1,即如图阴影部分的面积.
∴根据等可能事件的概率得到P=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查几何概型,古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、体积的比值得到.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目