题目内容
(本题满分14分)已知函数 其中a>0,且a≠1,
其中a>0,且a≠1,
(1)求函数 的定义域;
的定义域;
(2)当0<a<1时,解关于x的不等式 ;
;
(3)当a>1,且x∈[0,1)时,总有 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
(1)函数f(x)的定义域为 ;(2)
;(2) ;(3)m≤0。
;(3)m≤0。
【解析】
试题分析:(1)由真数大于零,可得函数的定义域.
(2)由f(x)≥0得2loga(x+1)≥loga(1-x),因为0<a<1,则对数函数是减函数,
所以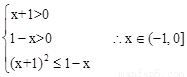 .
.
(3) a>1且x∈[0,1)时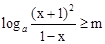 恒成立.
恒成立.
然后研究真数 的取值范围,再结合对数函数的单调性可求出
的取值范围,再结合对数函数的单调性可求出 的最小值,让m小于等于其最小值即可.
的最小值,让m小于等于其最小值即可.
(1) 函数f(x)的定义域为
函数f(x)的定义域为 ………3分
………3分
(2)由f(x)≥0得2loga(x+1)≥loga(1-x)
∵0<a<1 ∴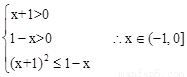 ……………………………………(8分)
……………………………………(8分)
(3)由题意知:a>1且x∈[0,1)时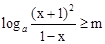 恒成立.……(9分)
恒成立.……(9分)
设 ,令t=1-x,t∈(0,1],∴
,令t=1-x,t∈(0,1],∴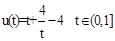 ……(10分)
……(10分)
设

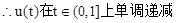 ,
,
∴u(t)的最小值为1……………………………(12分)
又∵a>1, 的最小值为0…………………(13分)
的最小值为0…………………(13分)
∴m的取值范围是m≤0…………………………………(14分)
考点: 对数函数的定义域,解对数不等式,对数函数的性质,不等式恒成立,对数函数的最值.
点评:对数的真数大于零,就是求函数的定义域的依据之一;
利用对数函数的单调性求解不等式转化为真数的大小关系;
不等式恒成立问题,在参数与变量分离的情况下可转化为函数的最值问题来解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
