题目内容
已知椭圆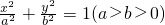 的离心率是
的离心率是 .
.
(1)证明:a=2b;
(2)设点P为椭圆上的动点,点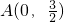 ,若
,若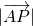 的最大值是
的最大值是 ,求椭圆的方程.
,求椭圆的方程.
解:(1)证明:设椭圆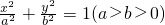 的半焦距为c.
的半焦距为c.
因为椭圆的离心率是 ,所以
,所以 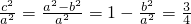 ,即a=2b.
,即a=2b.
(2)设点P(x,y).
则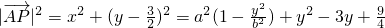 =
=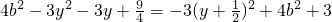 ,其中-b≤y≤b.
,其中-b≤y≤b.
①若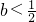 2,则当y=-b3时,
2,则当y=-b3时,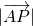 4取得最大值.
4取得最大值.
由题设,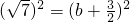 ,
,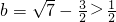 ,这与
,这与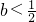 矛盾.
矛盾.
②若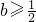 ,则当
,则当 时,
时,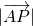 取得最大值.
取得最大值.
由题设,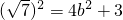 ,解得b=1,从而a=2.
,解得b=1,从而a=2.
故椭圆方程为 .
.
分析:(1)根据离心率为 =
= 以及c2=a2-b2,即可证明结论.
以及c2=a2-b2,即可证明结论.
(2)设P(x,y)由/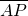 /的最大值为
/的最大值为 ,求得b的值,从而求得椭圆方程.
,求得b的值,从而求得椭圆方程.
点评:本题主要考查椭圆的基本性质,并渗透了向量、函数最值等问题,此题要注意对b的范围进行分类讨论,属于基础题.
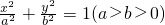 的半焦距为c.
的半焦距为c.因为椭圆的离心率是
 ,所以
,所以 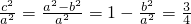 ,即a=2b.
,即a=2b. (2)设点P(x,y).
则
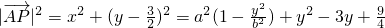 =
=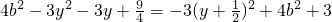 ,其中-b≤y≤b.
,其中-b≤y≤b.①若
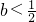 2,则当y=-b3时,
2,则当y=-b3时,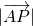 4取得最大值.
4取得最大值.由题设,
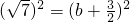 ,
,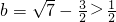 ,这与
,这与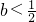 矛盾.
矛盾. ②若
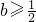 ,则当
,则当 时,
时,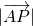 取得最大值.
取得最大值.由题设,
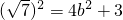 ,解得b=1,从而a=2.
,解得b=1,从而a=2.故椭圆方程为
 .
.分析:(1)根据离心率为
 =
= 以及c2=a2-b2,即可证明结论.
以及c2=a2-b2,即可证明结论.(2)设P(x,y)由/
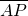 /的最大值为
/的最大值为 ,求得b的值,从而求得椭圆方程.
,求得b的值,从而求得椭圆方程.点评:本题主要考查椭圆的基本性质,并渗透了向量、函数最值等问题,此题要注意对b的范围进行分类讨论,属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
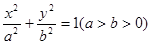 的离心率是
的离心率是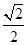 ,右焦点
,右焦点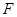 到上顶点的距离为
到上顶点的距离为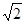 ,点
,点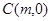 是线段
是线段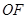 上的一个动点.
上的一个动点.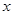 轴不垂直的直线
轴不垂直的直线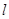 与椭圆交于
与椭圆交于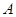 、
、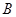 两点,使得
两点,使得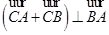 ,并说明理由.
,并说明理由. 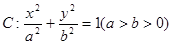 的离心率是
的离心率是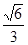 ,长轴长是为6,
,长轴长是为6,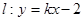 与
与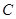 交于
交于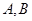 两点,已知点
两点,已知点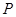 的坐标为
的坐标为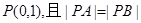 ,求直线
,求直线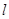 的方程。
的方程。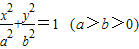 的离心率是
的离心率是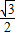 .
.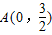 ,若
,若 的最大值是
的最大值是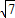 ,求椭圆的方程.
,求椭圆的方程.