题目内容
直线l与椭圆
+
=1(a>b>0)交于不同的两点M,N,过点M,N作x轴的垂线,垂足恰好是椭圆的两个焦点,已知椭圆的离心率是
,直线l的斜率存在且不为0,那么直线l的斜率是
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
±
| ||
| 2 |
±
.
| ||
| 2 |
分析:由椭圆
+
=1(a>b>0)的离心率是
,知a=2k,c=
k,b=
k,设椭圆的两个焦点横坐标是-c,c,则M(-c,-
),N(c,
),或M(-c,
),N(c,-
),由此能求出直线l的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| 2 |
| b2 |
| a |
| b2 |
| a |
| b2 |
| a |
| b2 |
| a |
解答:解:∵椭圆
+
=1(a>b>0)的离心率是
,
∴a=2k,c=
k,b=
k,
设椭圆的两个焦点横坐标是-c,c,
则M(-c,-
),N(c,
),或M(-c,
),N(c,-
),
当M(-c,-
),N(c,
)时,
直线l的斜率k=
=
=
=
;
当M(-c,
),N(c,-
)时,
直线l的斜率k=-
=-
=-
=-
.
故答案为:±
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴a=2k,c=
| 2 |
| 2 |
设椭圆的两个焦点横坐标是-c,c,
则M(-c,-
| b2 |
| a |
| b2 |
| a |
| b2 |
| a |
| b2 |
| a |
当M(-c,-
| b2 |
| a |
| b2 |
| a |
直线l的斜率k=
| ||
| 2c |
| b2 |
| ac |
| 2k2 | ||
2
|
| ||
| 2 |
当M(-c,
| b2 |
| a |
| b2 |
| a |
直线l的斜率k=-
| ||
| 2c |
| b2 |
| ac |
| 2k2 | ||
2
|
| ||
| 2 |
故答案为:±
| ||
| 2 |
点评:本题考查直线的斜式的求法,具体涉及到椭圆的简单性质及其应用、直线的斜率公式、直线与椭圆的位置关系等基本知识点,解题地要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
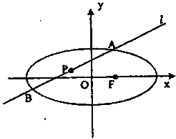 如图,设斜率为
如图,设斜率为